파이썬자료구조(20-23)이진탐색트리-힙

17강 트리

이진 탐색 트리 (Bianry Search Trees) - 원소 삽입 연산
이진 탐색 트리 (Bianry Search Trees) - 원소 삭제 연산
힙 (Heaps) - 최대 힙에 새로운 원소 삽입
힙 (Heaps) - 최대 힙에서의 원소 삭제

20 이진 탐색 트리 - Bianry Search Trees

모든 노드에 대해서
- 왼쪽 서브트리에 있는 데이터는 모두 현재 노드의 값보다 작고
- 오른쪽 서브트리에 있는 데이터는 모두 현재 노드의 값보다 큰 성질을 만족하는 이진트리
(중복되는 데이터 원소는 없는 것으로 가정)
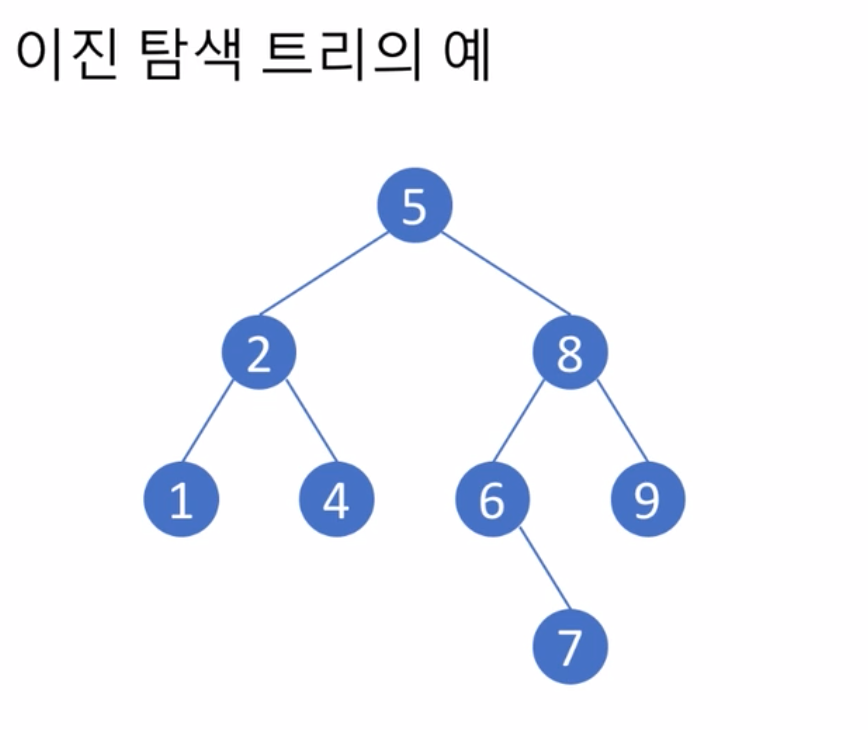
데이터 검색에 효율적으로 사용 가능
(정렬된 )배열을 이용한 이진 탐색 비교
이진 탐색 트리
장점 : 데이터의 원소 추가, 삭제가 용이
단점 : 공간 요소가 큼
항상 O(log n)의 탐색 복잡도 ? => 아니다.
이진 탐색 트리의 추상적 자료구조
데이터 표현 : 각 노드는 (key,value) 쌍으로
키를 이용해서 검색 가능
보다 복잡한 데이터 레코드로 확장 가능

연산의 정의

insert(key,data) - 트리에 주어진 데이터 원소를 추가
remove(key) - 특정 원소를 트리로부터 삭제
lookup(key) - 특정 원소를 검색
inorder() - 키의 순서대로 데이터 원소를 나열
min(), max() - 최소 키, 최대 키를 가지는 원소를 각각 탐색

코드 구현 - lookup()

입력 인자 :
- 찾으려는 대상 키
리턴:
- 찾은 노드와, 그것의 부모 노드 (각각, 없으면 None 으로)

코드 구현 - insert()

입력 인자 :
- 키, 데이터 원소
리턴 :
- 없음
주어진 키가 지금 방문된 노드 키보다 작은지 큰지에 따라서 왼쪽, 오른쪽 서브트리에 인서트 메소드를 호출하거나
마지막 까지 왔으면, 삽입할 위치를 된거니까. 새로운 노드를 만들어서 갖다 달면 된다.
그렇지 않다면 raise KeyError를 exception을 일으킨다.

def insert(self, key, data):
        if key < self.key:
            if self.left:
                self.left.insert(key, data)
            else:
                self.left = Node(key, data)
        elif key > self.key:
            if self.right:
                self.right.insert(key, data)
            else:
                self.right = Node(key, data)
        else:
            raise KeyError('Key %s already exists.' % key)

21. 이진 탐색 트리 - Binary Search Trees

키(key)를 이용해서 노드를 찾는다.
- 해당 키의 노드가 없으면, 삭제할 것도 없음
- 찾은 노드의 부모 노드도 알고 있어야 함 (아래 2번 때문)
찾은 노드를 제거하고도 이진 탐색 트리의 성질을 만족하도록 트리의 구조를 정리한다.

인터 페이스 설계

입력 : 키 (key) 출력 : 삭제한 경우 True 해당 키의 노드가 없는 경우 False

class BinSearchTree:
    def remove(self,key):
        node,parent = self.lookup(key)
        if node:
            ...
            return True
        else:
            return False

이진 탐색 트리 구조의 유지

삭제되는 노드가

말단(leaf)노드인 경우
- 그냥 그 노드를 없애면 됨 -> 부모 노드의 링크를 조정 (좌? 우?)
자식을 하나 가지는 경우
- 삭제되는 노드 자리에 그 자식을 대신 배치 -> 자식이 왼쪽? 오른쪽? -> 부모 노드의 링크를 조정(좌?우?)
자식을 둘 가지는 경우
- 삭제되는 노드보다 바로 다음 (큰) 키를 가지는 노드를 찾아 그 노드를 삭제되는 노드 자리에 대신 배치하고 이 노드를 대신 삭제

우선 자식을 세어 보자

class Node:
    def countchildren(self):
        count = 0
        if self.left:
            count +=1
        if self.right:
            count +=1
        return count

말단 노드의 삭제

삭제되는 노드(x)가 root node 경우는 어떻게 ? -> self.root=None을 대입하는 식이 될거야.

자식이 하나인 노드 삭제

지워야할 x 노드의 자식이 오른쪽인지, 왼쪽인지 판단해서 대신 x자리에 위치시키면 된다.
x의 부모노드인 p의 링크도 지정해줘야 하기 때문에 x의 부모노드 또한 알고 있어야 한다.
삭제되는 노드 x가 root node인 경우는 -> 대신 들어오는 자식이 root가 됌

자식이 둘인 노드의 삭제

5를 삭제해라 ? -> 5에 해당하는 걸 찾으면 삭제될 노드 x는 5
5의 삭제되려는 노드의 오른쪽 자식으로 시작해서 왼쪽을 따라가다보면, 5보다 한칸 더 큰 키를 찾게 된다.
그런 노드를 successor라고 불러서 s라고 표시.
그리고 그 successor의 부모 P도 알고 있어야 한다.
successor의 6을 삭제되려는 노드 x에 대신 집어 넣는다.
그 후 6을 대신 삭제하면 된다.
왼쪽 차일드는 없을 수 밖에 없다. minimum을 찾았기에,
그렇기 때문에 successor의 오른쪽 자식을 P의 왼쪽으로 자식으로 만들면 된다.
그런데, 8을 삭제한다고 가정한다면 ?
아까 코드 구현과는 조금 다르다. successor노드가 9가 되는데, 9는 8의 오른쪽 자식
그렇다면 succesor의 parent는 x와 같은 노드,
9를 x 자리에 넣고, 9에 오른쪽 링크를 조절해야 한다.
if 조건문을 이용해서 이 조건을 해줘야 한다.

이진 탐색 트리가 별로 효율적이지 못한 경우

T = BinSearchTree()
T.insert(1,'John')
T.insert(2,'Mary')
T.insert(3,'Anne')
T.insert(4,'Peter')

선형 탐색과 동등한 시간 복잡도 발생 (Screwed Tree)

보다 나은 성능을 보이는 이진 탐색 트리들

높이의 균형을 유지함으로써 O(log n)의 탐색 복잡도 보장. 삽입, 삭제 연산이 복잡
AVLTree
Red-black-tree

실습문제

class Node:

    def __init__(self, key, data):
        self.key = key
        self.data = data
        self.left = None
        self.right = None


    def insert(self, key, data):
        if key < self.key:
            if self.left:
                self.left.insert(key, data)
            else:
                self.left = Node(key, data)
        elif key > self.key:
            if self.right:
                self.right.insert(key, data)
            else:
                self.right = Node(key, data)
        else:
            raise KeyError('Key %s already exists.' % key)


    def lookup(self, key, parent=None):
        if key < self.key:
            if self.left:
                return self.left.lookup(key, self)
            else:
                return None, None
        elif key > self.key:
            if self.right:
                return self.right.lookup(key, self)
            else:
                return None, None
        else:
            return self, parent


    def inorder(self):
        traversal = []
        if self.left:
            traversal += self.left.inorder()
        traversal.append(self)
        if self.right:
            traversal += self.right.inorder()
        return traversal


    def countChildren(self):
        count = 0
        if self.left:
            count += 1
        if self.right:
            count += 1
        return count


class BinSearchTree:

    def __init__(self):
        self.root = None


    def insert(self, key, data):
        if self.root:
            self.root.insert(key, data)
        else:
            self.root = Node(key, data)


    def lookup(self, key):
        if self.root:
            return self.root.lookup(key)
        else:
            return None, None


    def remove(self, key):
        node, parent = self.lookup(key)
        if node:
            nChildren = node.countChildren()
            # The simplest case of no children
            if nChildren == 0:
                # 만약 parent 가 있으면
                # node 가 왼쪽 자식인지 오른쪽 자식인지 판단하여
                # parent.left 또는 parent.right 를 None 으로 하여
                # leaf node 였던 자식을 트리에서 끊어내어 없앱니다.
                if parent:
                    if parent.key>node.key:
                        parent.left=None
                    else:
                        parent.right=None
                # 만약 parent 가 없으면 (node 는 root 인 경우)
                # self.root 를 None 으로 하여 빈 트리로 만듭니다.
                else:
                    self.root=None
            # When the node has only one child
            elif nChildren == 1:
                # 하나 있는 자식이 왼쪽인지 오른쪽인지를 판단하여
                # 그 자식을 어떤 변수가 가리키도록 합니다.
                if node.left:
                    child=node.left
                else:
                    child=node.right
                # 만약 parent 가 있으면
                # node 가 왼쪽 자식인지 오른쪽 자식인지 판단하여
                # 위에서 가리킨 자식을 대신 node 의 자리에 넣습니다.
                if parent:
                    if parent.key>node.key:
                        parent.left=child
                    else:
                        parent.right=child
                # 만약 parent 가 없으면 (node 는 root 인 경우)
                # self.root 에 위에서 가리킨 자식을 대신 넣습니다.
                else:
                    self.root=child

            # When the node has both left and right children
            else:
                parent = node
                successor = node.right
                # parent 는 node 를 가리키고 있고,
                # successor 는 node 의 오른쪽 자식을 가리키고 있으므로
                # successor 로부터 왼쪽 자식의 링크를 반복하여 따라감으로써
                # 순환문이 종료할 때 successor 는 바로 다음 키를 가진 노드를,
                # 그리고 parent 는 그 노드의 부모 노드를 가리키도록 찾아냅니다.
                while successor.left:
                    parent=successor
                    successor=successor.left

                # 삭제하려는 노드인 node 에 successor 의 key 와 data 를 대입합니다.
                node.key = successor.key
                node.data = successor.data
                # 이제, successor 가 parent 의 왼쪽 자식인지 오른쪽 자식인지를 판단하여
                # 그에 따라 parent.left 또는 parent.right 를
                # successor 가 가지고 있던 (없을 수도 있지만) 자식을 가리키도록 합니다.
                if parent.key>node.key:
                    parent.left=None
                else:
                    parent.right=None
            return True
        else:
            return False



    def inorder(self):
        if self.root:
            return self.root.inorder()
        else:
            return []


def solution(x):
    return 0

22. 힙 - heaps

힙(heap)이란 ?
이진 트리의 한 종류 (이진 힙- binaray heap)

루트(root) 노드가 언제나 최댓값 또는 최솟값을 가짐
- 최대 힙(max heap), 최소 힙 (min heap)
완전 이진트리여야 한다.

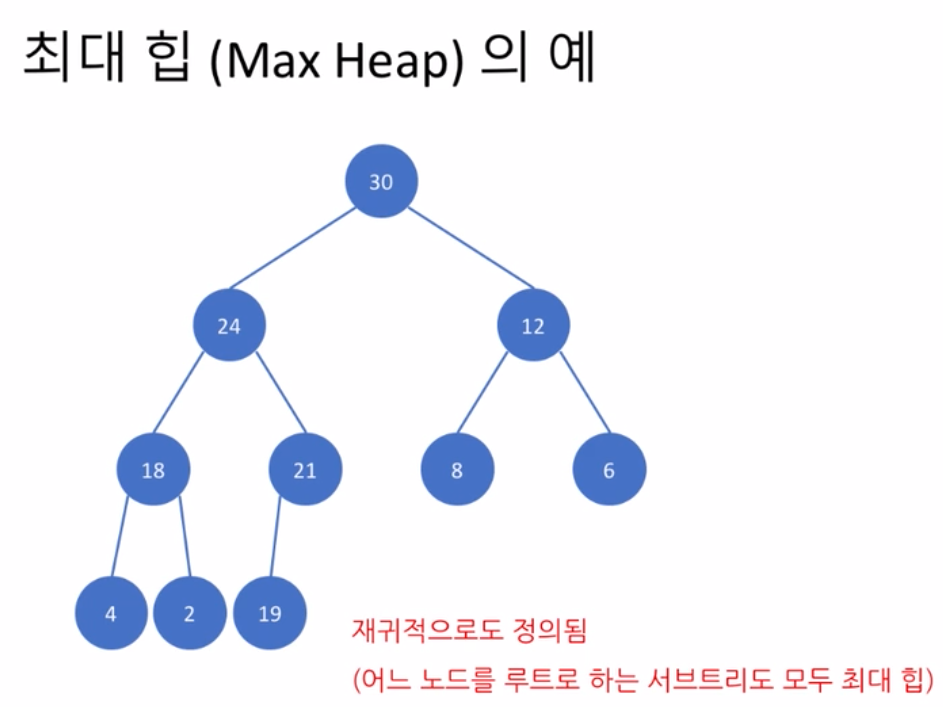
느슨한 정렬 구조를 가짐 (좌,우 크기가 완전 정렬 x)

이진 탐색트리와의 비교

원소들은 완전히 크기 순으로 정렬되어 있는가?
- 힙은 이진 탐색 트리에 비해 느슨하게 정렬되어 있다.
특정 키값을 가지는 원소를 빠르게 검색할 수 있는가?
- 이진 탐색 트리는 빠르게 검색이 가능하다.
- 힙은 특정한 키값을 검색하는데 별로 좋은 방법이 없다.
부가의 제약 조건은 어떤 것인가?
- 힙은 BST에 비해 완전 이진트리여야 한다는 제약조건을 가짐

최대힙의 추상적 자료구조

연산의 정의
init()빈 최대 힙을 생성
insert(item) - 새로운 원소를 삽입
remove() - 최대 원소(root node)를 반환 ( 그리고 동시에 이 노드를 삭제)
BST와 달리 search와 traverse와 같은 연산들은 제공하지 않는다.

데이터 표현의 설계

배열을 이용한 이진 트리의 표현
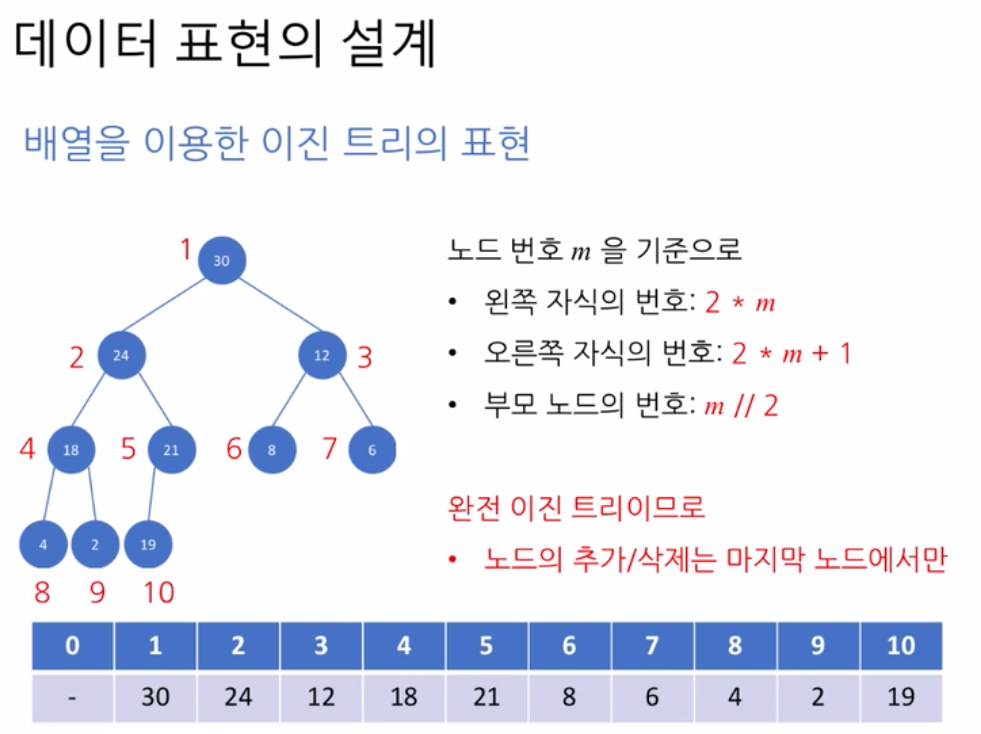
완전 이진트리의 성질을 만족하기에 배열로 표현하기 적합하다.

코드 구현 - 빈 힙 생성

class MaxHeap:
    def __init__(self):
        self.data = [None]

최대 힙에 원소 삽입

트리의 마지막 자리에 새로운 원소를 임시로 저장
부모 노드와 키값을 비교하여 위로, 위로 이동

최대 힙에 원소 삽입 - 복잡도

원소의 개수가 n인 최대 힙에 새로운 원소 삽입
부모 노드와의 대소 비교 최대 회수 : logn
따라서 최악의 보갖ㅂ도가 O(log n)의 삽입 연산

삽입 연산의 구현 - insert(item) 메서드

class MaxHeap:
    def insert(self,item):

힌트: python에서 두 변수의 값 바꾸기

a=3,b=5 a,b = b,a

실습문제

class MaxHeap:

    def __init__(self):
        self.data = [None]


    def insert(self, item):
        self.data.append(item) # 마지막에 임시로 원소 추가
        i = len(self.data) -1 # 마지막 인덱스 기억
        while i >1 : #루트까지
            if self.data[i] > self.data[i//2]: # 부모 노드의 번호 : m//2
                self.data[i],self.data[i//2] = self.data[i//2],self.data[i]
                i = i//2
            else:
                break

def solution(x):
    return 0

23. 힙 - heaps

최대 힙에서의 원소의 삭제

루트노드의 제거 - 이것이 원소들 중 최댓값 (루트노드를 빼내면 완전이진트리가 될 수 없다 따라서)
트리 마지막 자리 노드를 임시로 루트 노드의 자리에 배치 (완전 이진트리 모양은 갖춤)
자식 노드들과의 값 비교와 아래로, 아래로 이동
- 자식은 둘 있을 수도 있는데, 어느 쪽으로 이동?

최대 힙에서의 삭제 예

루트 노드의 제거 - 이것이 원소들 중 최댓값
트리 마지막 자리 노드를 임시로 루트 노드의 자리에 배치
자식 노드들과의 값 비교와 아래로, 아래로 이동
- 더 큰 키 값을 가지는 쪽으로!

최대 힙으로부터 원소 삭제 - 복잡도

원소의 개수가 n인 최대 힙에서 최대 원소 삭제
자식 노드들과의 대소 비교 최대 회수 :2 * log n
최악 복잡도 O(log n) 삭제 연산

삭제 연산의 구현 remove 메서드

class MaxHeap:
    def remove(self):
        if len (self.data)> 1:
            self.data[1],self.data[-1] = self.data[-1],self.data[-1]
            data.self.data.pop[-1]
            self.maxHeapify(1)
        else:
            data = None
        return data

삭제 연산의 구현 - maxHeapify() 메서드

class MaxHeap:
    def maxHeapify(self,i):
        left = ...
        right = ...
        smallest = i
        # 자식 (i), 왼쪽 자식 (left), 오른쪽 자식(right) 중 최대를 찾음
        # -> 이것의 인덱스를 smallest에 담음
        if smallest != i:
            # 현재 노드 i와 최댓값 smallest의 값 바꾸기
            # 재귀적으로 maxHeapify를 호출

최대/최소 힙의 응용

우선 순위 큐 (priority Queue)
- enqueue할 때, 느슨한 정렬을 이루고 있도록 함 : O(log n)
- dequeue할 때, 최댓값을 순서대로 추출 : O(log n)
- 제 16강에서의 양방향 연결 리스트 이용 구현과 효율성 비교
힙 정렬 (Sort)
- 정렬되지 않은 원소들을 아무 순서로나 최대 힙에 삽입: O(log n)
- 삽입이 끝나면, 힙이 비게될 때까지 하나씩 삭제 : O(log n)
- 원소들이 삭제된 순서가 원소들의 정렬 순서
- 정렬 알고리즘의 복잡도 O(log n)

힙 정렬의 코드 구현

def heapsort(unsorted):
    H = MaxHeap()
    for item in unsorted:
        H.insert(item)
    sorted = []
    d = H.remove()
    while d:
        sorted.append(d)
        d = H.remove()
    return sorted

실습문제

 def maxHeapify(self, i):
        # 왼쪽 자식 (left child) 의 인덱스를 계산합니다.
        left =i*2

        # 오른쪽 자식 (right child) 의 인덱스를 계산합니다.
        right =2*i+1

        smallest = i
        # 왼쪽 자식이 존재하는지, 그리고 왼쪽 자식의 (키) 값이 (무엇보다?) 더 큰지를 판단합니다.
        if left <len(self.data) and self.data[left] > self.data[smallest] :
            # 조건이 만족하는 경우, smallest 는 왼쪽 자식의 인덱스를 가집니다.
            smallest = left

        # 오른쪽 자식이 존재하는지, 그리고 오른쪽 자식의 (키) 값이 (무엇보다?) 더 큰지를 판단합니다.
        if right < len(self.data) and self.data[right] > self.data[smallest]:
            # 조건이 만족하는 경우, smallest 는 오른쪽 자식의 인덱스를 가집니다.
            smallest = right

        if smallest != i:
            # 현재 노드 (인덱스 i) 와 최댓값 노드 (왼쪽 아니면 오른쪽 자식) 를 교체합니다.
            self.data[smallest], self.data[i] = self.data[i], self.data[smallest]

            # 재귀적 호출을 이용하여 최대 힙의 성질을 만족할 때까지 트리를 정리합니다.
            self.maxHeapify(smallest)

참고자료 [파이썬_자료구조_알고리즘]https://programmers.co.kr/learn/courses/57