SWE 완전검색
- Baby-Gin여부 판단
- 가장 쉬운 방법은 완전 검색
-
고지식한 방법(Brute-force)이라고도 함
- BabyGin의 경우 모든 경우의 수 생성하기 (6개의 숫자 중 3개를 생성하는 모든 경우의 수)
- 앞, 뒤 세자리 잘라서 최종적으로 베이비 - 진 판단
-
BabyGin의 중복을 제거할 수 있다면 계산시간 단축 가능
- 조합적 문제 (순열, 조합, 부분집합과 같은)
- 완전 검색은 조합적 문제에 대한 고지식한 방법
-
순열 : 서로 다른 것들 중 몇 개를 뽑아서 한 줄로 나열하는 것. (nPr)
- {1,2,3,4} 순열 생성
- 첫 번째 위치에 대한 요소 선택 : 나머지 요소들로 순열 생성. 남아있는 요소로 생성할 수 있는 6가지,
- 다음은 남은 3과 4로 생성 ->
- 즉 깊이가 4이고, 단말 노드의 수가 24개인 트리 구조가 된다.
- 순서화된 요소들의 집합에서 최선의 방법을 찾는 것과 관련됨
-
출발도시에서 시작해서 다른 모든 도시들을 단 한번만 방문하고 돌아올 때, 최소비용의 이동경로를 구하는 순회외판원 문제각 대표문제
- 단순하게 순열을 생성하는 함수 -> for 루프 중첩
- Baby-Gin을 판별하는 프로그램은 6개의 루프 중첩으로 가능
-
순열 수가 고정되지 않는다면 이런 방식은 어려우니, 재귀 호출을 이용해서 필요한 횟수만큼 반복수행
-
사전식 순서와 최소 변경을 통한 방법 (각각의 순열들은 이전의 상태에서 두 개의 요소들을 교환해서 생성)
- Johnson-Trotter 알고리즘
-
각 선들은 네 개의 요소에 대응되고, 점이 표시된 선이 교환되는 요소들을 의미
- 두 원소의 교환을 통해 생성
- n개의 요소가 있을 때, n번의 선택으로 순열 생성
# 재귀 호출을 통한 순열 생성 수도코드
# a[] : 데이터가 저장된 리스트
# n: 원소의 개수, k: 현재까지 선택된 원소의 수
def perm(n,k):
if k == n: # 하나의 순열이 생성됨
print(a) # 원하는 작업 수행
else:
for i in range(k,n):
a[k], a[i] = a[i],a[k] #교환을 통한 선택
print(n,k+1) # 재귀호출
a[k],a[i] = a[i],a[k] # 이전 상태로 복귀
# 파이썬 라이브러리를 활용한 순열
import itertools
mylist = [1,2,3]
result = itertools.permutations(mylist) # #생략시 기본값 리스트 크기
# 파이썬의 라이브러리를 활용한 중복순열
result = itertools.product(mylist,repeat=3)
- 부분집합
- 다수의 중요 알고리즘들이 원소들의 그룹에서 최적의 부분집합을 찾는 것
- 대표 문제 knapsack problem
- 단순하게 모든 부분집합 생성하는 방법
- 각 원소가 부분집합에 포함되어 있는지 반복문을 이용해 생성.
- shift연산을 통해 바이너리 카운팅을 하여 부분집합의 개수를 쉽게 구할 수 있다.
arr = [2,3,4,5]
n = len(arr)
for i in range(1<<n): # 1 <<n : 부분집합의 개수
for j in range(n): # 원소의 수만큼 비트를 비교함
if i & (1<<j) : # i의 j번째 비트가 1이면 j번째 원소 출력
print(arr[j],end=",")
print()
- 조합
- 서로 다른 n개의 원소 중 r개를 순서 없이 골라낸 것
- 재귀적 정의의 표현
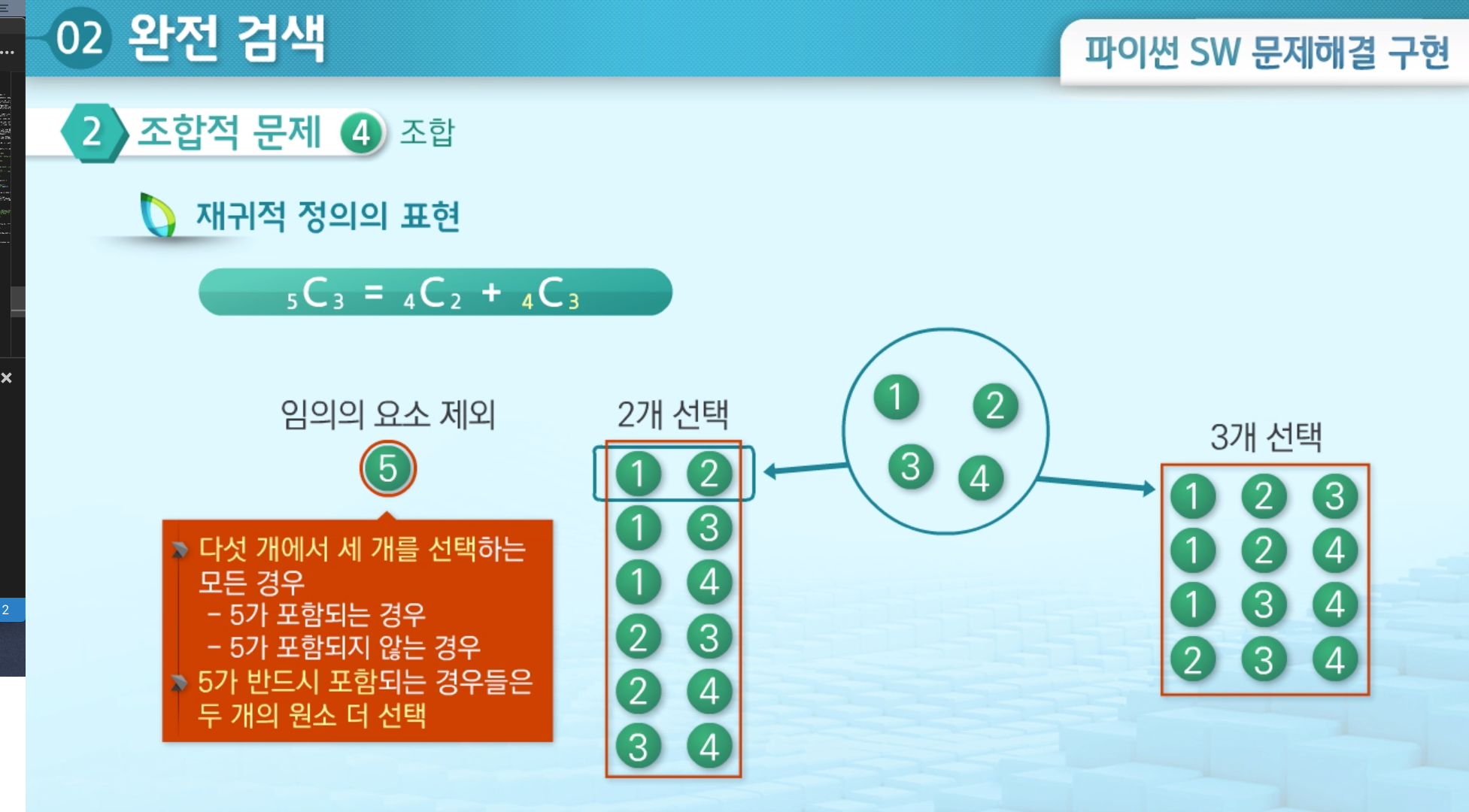
- 5C3 = 4C2 + 4C3
- 다섯 개에서 세 개를 선택하는 모든 경우
- 5가 포함되는 경우
- 5가 포함되지 않는 경우
-
5가 반드시 포함되는 경우들은 두 개의 원소 더 선택하면 된다.

-
- 재귀 호출을 이용한 조합 생성 알고리즘
# an[] : n개의 원소를 가지고 있는 리스트
# tr[] : 조합이 임시 저장될 r개의 크기의 리스트
def comb(n,r):
if r == 0: print(tr)
elif n < r : return
else:
tr[r-1] = an[n-1]
comb(n-1,r-1)
comb(n-1,r)
- 조합 라이브러리
# 파이썬 라이브러리를 활용한 조합
import itertools
mylist = [1,2,3]
result = itertools.combinations(mylist,r=2) # r은 생략불가
# 파이썬의 라이브러리를 활용한 중복조합
result = itertools.combinations_with_replacement(mylist,r=2) # r은 생략불가
참고자료 [SWexperacademy]https://swexpertacademy.com