파이썬_고득점키트_문제풀이(7)DFS,BFS_여행경로

작성일 | In

7. DFS,BFS 대표문제 - 여행경로

  • 그래프에 기반한 문제

배경지식

  • 그래프
    • 정점(vertex,node)과 간선(edge,link)
    • 유향(directed) 그래프와 무향 (undirected)그래프
  • 스택(stack)
  • 큐(queue)
  • 한 정점에서 인접한 모든 (아직 방문하지 않은) 정점을 방문하되,
    • 각 인접 정점을 기준으로 깊이 우선 탐색을 끝낸 후 다음 정점으로 진행

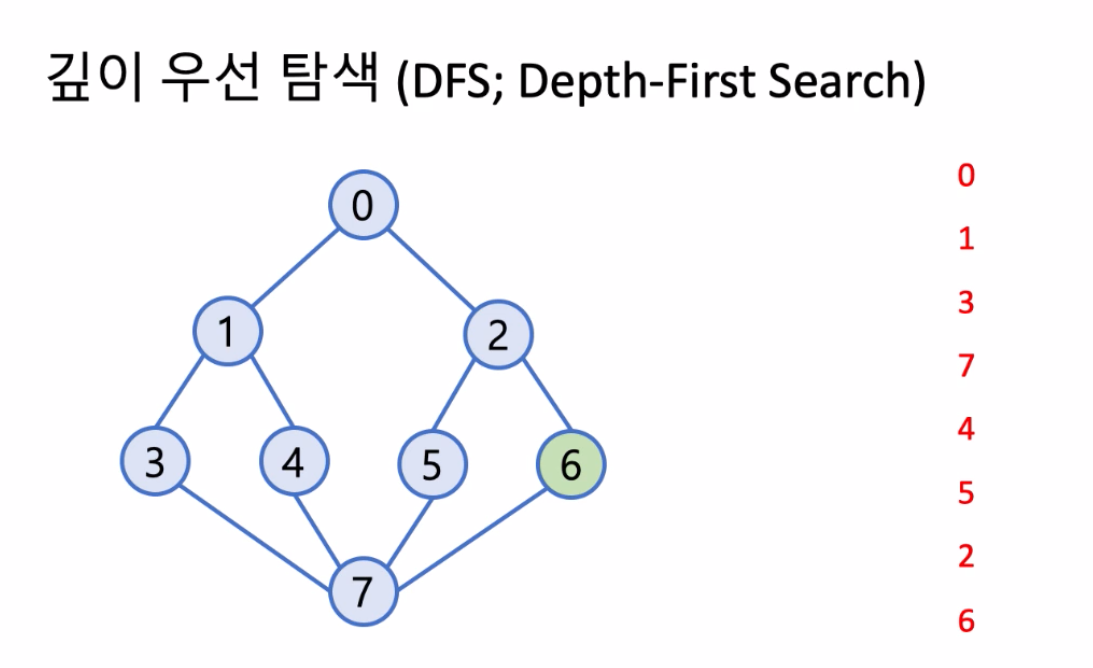
No Image

  • 위 방법이 유일한 방법은 아니다.
  • 스택을 이용하여 어느 정점에서 DFS를 하고 있는지를 기억하고 되돌아가는게 필요
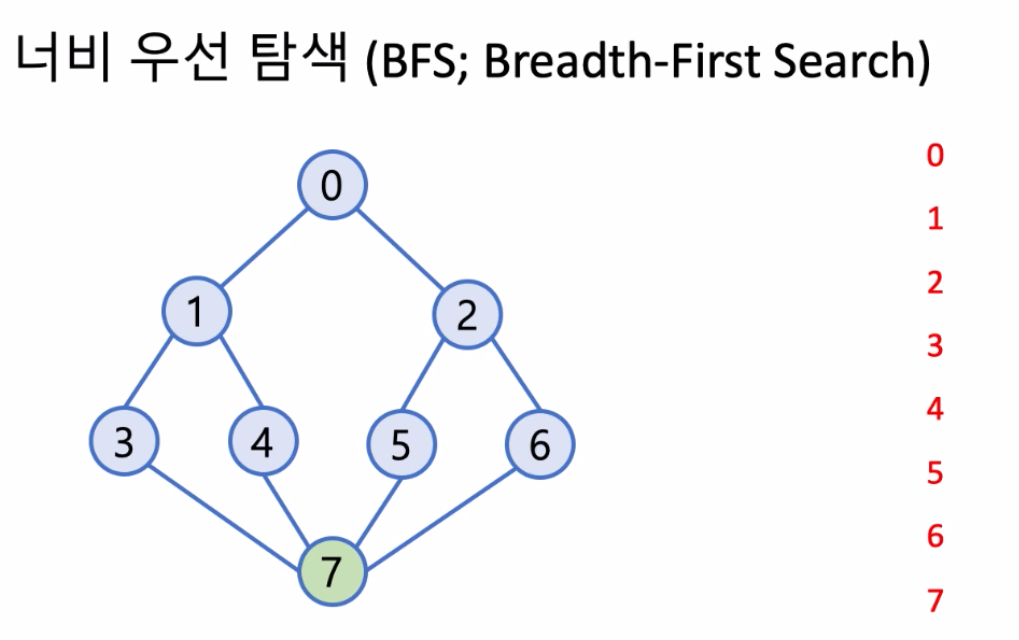
  • 한 정점에서 인접한 모든 (아직 방문하지 않은) 정점을 방문하고, - 방문한 각 인접 정점을 기준으로(방문한 순서에 따라) 또 다시 너비 우선 탐색을 행함 No Image
  • 위 방법이 유일한 방법은 아니다.
  • 이 모습을 가만히 보면, 아까 깊이 우선 탐색이 스택을 이용해서 깊이를 이용해서 되돌아가는 성질이 있었다면,
  • 큐를 이용하여 어느 정점에서 BFS를 해야하는지를 기록하고 진행함

문제해석

  • 주어진 항공권을 모듀 이용하여 여행 경로. 항상 “ICN” (인천공항)에서 출발

  • 항공권 정보가 담긴 2차원 배열 tickets가 매개변수로 주어질 때, 방문하는 공항 경로를 배열에 담아 return

  • 공항들이 정점이 되고, 항공권이 출발 공항과 도착 공항을 연결하는 항공권이 간선이 된다.

  • 제한사항
  • 모든 공항은 알파벳 대문자 3글자로 이루어진다.
  • 주어진 공항의 수는 3개 이상 10,000개 이하
  • tickets의 각 행 [a,b]는 a공항에서 b공항으로 가는 항공권이 있다는 의미
  • 주어진 항공권은 모두 사용해야 한다.
  • 가능한 경로가 2개 이상일 경우 알파벳 순서가 앞서는 경로를 return 한다
  • 모든 도시를 방문할 수 없는 경우는 주어지지 않는다.

예제 풀이

  • ICN -> JFK -> HND -> IAD

  • ICN -> ATL -> ICN -> SFO -> ATL -> SFO 이게 답이래. 즉 한붓그리기를 하고 있네.
  • 이게 유일한 가능한 경로는 아니다.
  • ICN -> ATL -> SFO -> ATL -> ICN -> SFO에서 끝내면 이것도 하나의 유효한 한붓그리기가 된다.
  • 위와 비교하면, 3번째 방문한 공항이 SFO고 아까 만든 건 ICN이다. 알파벳 순서로 ICN이 SFO보다 앞서므로 후자가 아닌 전자를 택해야 한다.

문제의 해결 - 깊이 우선 탐색(DFS)을 응용

  • 한붓 그리기!
    • 이것이 가능함은 문제에서 보장되어 있다.
  • 시작 정점은 언제나 “ICN”
  • 모든 정점 방문이 아니고, 모든 간선을 거쳐야
    • 언젠가는 한번 가야하는데, 그 순서를 결정하라
  • 한 정점에서 택할 수 있는 간선이 두 개 이상인 겨우?
    • 공항 이름의 알파벳 순서를 따른다.

알고리즘의 설계

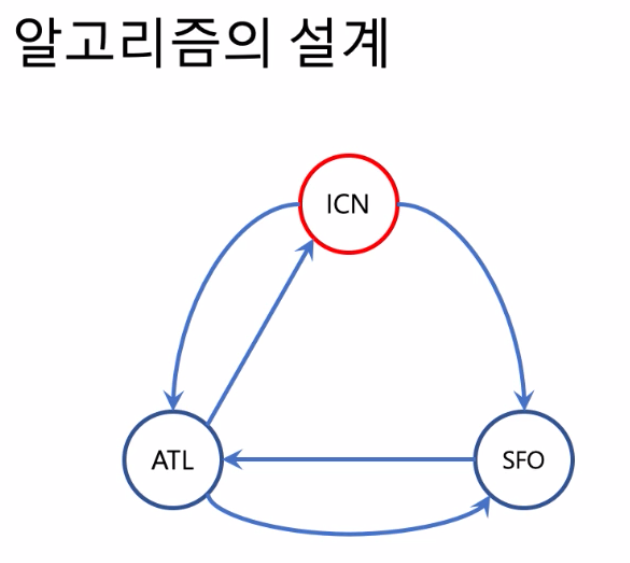
  • 인천공항에서 출발. No Image
  • ICN에서 갈 수 있는 곳은 ATL와 SFO가 있다.
  • 그 중 알파벳 순서가 앞서는 ATL를 선택하고
  • 이 항공권은 썼으니까 없는 것으로 치고
  • ATL에서 시작해서 지금 남은 항공권만 가지고, 알파벳 순서로 가장 빠르게 할 수 있는 한붓 그리기를 해라와 도일한 문제 - 재귀적 느낌
  • ICN과 SFO가 있다. 그 중 알파벳이 앞선 ICN 선택. 쓴 항공권 없애고

  • 나머지 ICN에서 갈 수 있는 곳은 SFO …

  • 스택을 이용하여 재귀적인 “한 붓 그리기” 문제를 해결 -> DFS 알고리즘의 응용

알고리즘의 동작

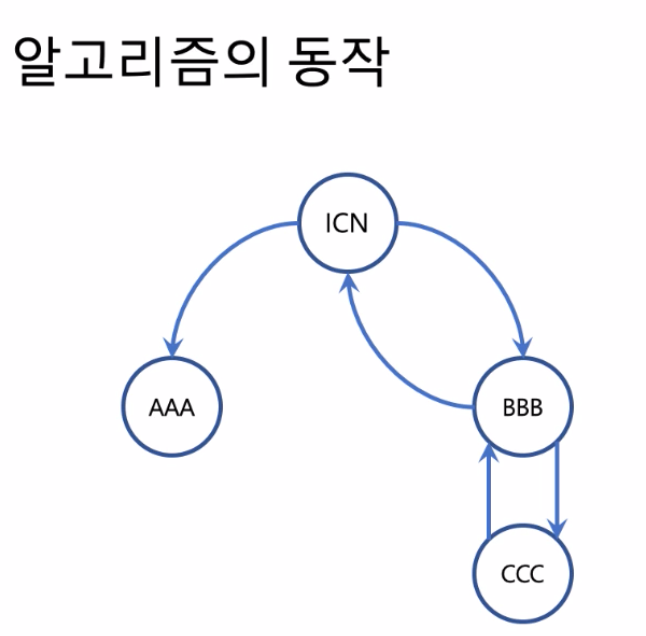
No Image

  • 시작은 인천공항. 방문하는 공항을 스택에 집어 넣는다.-> ICN을 넣는다.
  • 인천공항에서 갈 수 있는 공항은 AAA와 BBB가 있는데, AAA가 알파벳 순서가 우선하므로 AAA를 스택에 집어 넣는다.
  • AAA를 넣었는데 갈 수 있는 곳이 없네 ? AAA를 꺼내서 어딘가에 적어둔다.
  • 원래 공항인 인천공항에 돌아와서 나머지 DFS를 한다.
  • BBB를 택하고, BBB에서는 갈 수 있는 곳이 ICN과 CCC가 있는데 알파벳 순서가 CCC가 우선하므로
  • CCC를 가고, CCC를 스택에 담는다.
  • CCC에서 갈 수 있는 곳은 한 군데가 있다. BBB가 있으니, BBB로 방문 스택에 넣는다.

  • 이제 남아있는 곳 ICN으로 간다. ICN을 스택에 담는다.

  • 이게 끝이다.라고 판단하고 스택에서 꺼내기 시작한다.
  • 그런데 한붓 그리기도 실패할 수 있는 경우도 있나 ? -> 문제에서 되지 않는 케이스는 주지 않는다고 했다.
  • 마지막 더이상 표가 남아 있지 않게 되버리면 한붓 그리기가 성공한거다.
  • 스택에서 하나씩 빼서
  • AAA - ICN - BBB - CCC - BBB - ICN
  • 이 순서는 방문한 공항들의 역순이다. 스택에서 꺼낸 것의 역순으로 순서를 매기면, 우리가 주어진 문제에서 요구하는 경로를 찾아낸 셈이 된다.

요약

  • 그래프 문제가 주어지면, 복잡하고 어렵다는 생각이 들지만, 이 문제는 단순한 편이다.
  • 재귀적인 성질을 가진 “한 붓 그리기” 문제
    • 재귀적인 성질을 가진 “ 그래프의 깊이 우선 탐색”을 응용하여 해결
    • 스택을 이용했는데, 스택에 방문한 공항을 집어 넣고, 그 공항에 도착한 항공권은 없는 걸로 치고, 거기서부터 시작해서 한 붓 그리기 문제를 풀면, 그 문제랑 아까 나한테 도달하기 전에 왔던 공항은 나보다 스택에서 밑에 있기 때문에, 표가 없어진 걸로 치고 나머지 문제를 풀어서 다시 나한테 도달했던 전 상황까지 복귀하면, 스택을 이용한 전체의 답이 알파벳 순서를 우선적으로 하면서, 모든 공항들을 방문하는 경로. 즉 답이 된다.

코드 구현

  • 코드 작성 전에 ,그래프를 어떻게 코드로 표현할지 생각해보자.
  • 사전을 이용하여, 각 공항에서 출발하는 항공권의 집합을 표현하려고 한다.
  • 예를 들면 ICN -> {ATL,SFO}
  • 그럼 ICN이 key가 되고 {ATL,SFO}가 value가 된다.
  • ATL -> {ICN,SFO}
  • SFO -> {ATL}
  • 그래프를 방문하느데 알파벳 순서가 중요했다.
  • 따라서 집합이 아닌 리스트로 만드는게 유리할 것 같다.
  • 리스트에서 앞에서부터 원소를 제거하는 것 보다, 뒤에서 제거하는게 더 효율적이기 때문에,
  • 알파벳의 역순으로 정렬하겠다.
def solution(tickets):
    routes = {}
    for t in tickets:
        # 출발 공항이 키, value는 갈 수 있는 공항 들어있는 리스트
        routes[t[0]] = routes.get(t[0], []) + [t[1]]
    for r in routes:
        routes[r].sort(reverse=True)
    stack = ["ICN"]  # 빈 걸로 초기화할 수도 있지만 무조건 ICN은 넣어서 시작하므로
    path = []  # 가려고 하는 경로 표현
    while len(stack) > 0:  # stack이 다 없어질 때까지
        top = stack[-1]
        # 어떤 공항에서 출발하는 표가 한장도 없다면 또는 있었는데, 다 써버렸다면
        if top not in routes or len(routes[top]) == 0:
            path.append(stack.pop())
        else:
            stack.append(routes[top][-1])  # 역순으로 정렬을 해놨으니, 가장 앞서는
            # -1 직전까지 슬라이스를 해서, 떼어낸다. pop을 적용해도 된다.
            routes[top] = routes[top][:-1]
    return path[::-1]  # 역순- [start,end,step]이므로


print(solution([["ICN", "JFK"], ["HND", "IAD"], ["JFK", "HND"]]	))
  • 모든 목적지 공항에 해당하는 표가, 스택에 한번씩 들어가고, 스택에서 한번씩 꺼내진다.
  • 스택에 들어가고 나오는 횟수는 들어가고 한번, 나오고 한번. 즉 그 반복 횟수는 표의 개수에 비례한다.
  • 매번 표에 대해서 조사를 할 때, 무조건 리스트의 맨 끝에 있는 것을 꺼낸다.
  • 정렬되어 있지 않았다면, 표들을 다 봐야하기 때문에, 점근적으로 표현하면 n^2에 비례하는 알고리즘이 되는데,
  • 이 알고리즘의 복잡도는 nlogn이 된다. sort를 했기 때문이다.
  • 9행부터 시작하는 순환문의 경우에는, 모든 표를 하나씩 꺼내기 때문에, 이것의 반복 횟수는 표 개수만큼 이지만, 각 단계에서는 이미 정렬되어 있는 성질을 이용해서 각 단계는 상수시간에서 이루어진다.
  • 9행부터 시작되는 알고리즘은 linear 하다.
  • 재귀적 성질을 가지므로 스택을 이용해서 그래프에서 깊이우선 탐색을 하는 것처럼 문제를 풀었다.

참고자료 [프로그래머스]https://programmers.co.kr/learn/courses/9877

0%