파이썬_고득점키트_문제풀이(6)_DP

6. 동적계획법(Dp): N으로 표현

동적계획법이 어떤 것인지 이해하면, 다른 문제들도 쉽게 풀 수 있다.
동적계획법 (Dynamic Programming)
문제의 답인지를 확인하기 위해서, 탐색해야하는 범위를 어떤 부분을 탐색할 것인지에 진전하면서, 동적으로 결정한다라는 뜻이에서 다이나믹 프로그래밍이라고 한다.
주어진 최적화 문제를
- 재귀적인 방식으로 보다 작은 부분 문제로 나누어
- 부분 문제를 풀어 이 해를 조합하여
- 전체 문제의 해답에 이르는 방식
알고리즘의 진행에 따라 탐색해야 할 범위를 동적으로 결정함으로써
탐색 범위를 한정할 수 있음

동적 계획법의 적용 예

피보나치 수열 -> 재귀 함수로 구현한다면?
같은 인자로 함수 호출이 여러번 발생하는 문제.
복잡도: 지수 함수의 형태
피보나치 수열 -> 동적계획법을 적용한다면?
부분 해를 구한다. -> 그 해를 조합해서 전체문제를 푼다.
복잡도 : 선형 함수의 형태
Knapsack Problem
가장 높은 값을 가지도록 물건들을 골라 배낭에 담으시오
배낭에 15kg까지 담을 수 있는데 무엇을 담아야 가장 가치가 커지겠는가 ?
재귀적인 방법 가능.

N으로 표현 문제 접근

5와 사칙연산만으로 12를 표현할 수 있다.
12 = 5+5+(5/5)+(5/5)
12 - 55/5 + 5/5
12 = (55+5)/5
5를 사용한 횟수는 각각 6,5,4입니다. 그리고 이중 가장 작은 경우는 4입니다.
이처럼 숫자 N과 number가 주어질 때, N과 사칙연사만 사용해서 표현할 수 있는 방법 중에서 N 사용 횟수와의 최솟값을 return 하도록 하는 함수를 작성하세요
제한사항
N은 1이상 9이하
number는 1이상 32000이하
수식에는 괄호와 사칙연산만 가능하며 나누기 연산에서 나머지는 무시
최솟값이 8보다 크면 -1을 리턴한다.
입출력 예 설명
5 12 4
2 11 3

문제의 해결 - 동적계획법으로 설계

N을 한 번 사용해서 만들 수 있는 수들 -> 1
N을 2번 사용해서 만들 수 있는 수들 -> 2
N을 3번 사용해서 만들 수 있는 수들 -> 3

문제의 해결 - 예제

N=5인 경우에는
1번 5를 사용해서 만들 수 있는 수는 5 밖에 없다
2 : 55(일단 55가 있고) /
- 1 +-*/ 1 (한번 사용해서 만든 수를 앞뒤로 놓고 사칙연산을 하면 구할 수 있다)
- 그 결과는 10 0 25 1이다.
3 : 555 (일단 555가 있고)
- 1 +-*/ 2
- 2 +-*/ 2
- +와 *는 교환법칙이 성립해서 마찬가지이긴 하나, 개념적으로 깔끔하게 보이기 위해서.
- 그리고 2번 계산하지 않기 위해서 집합으로 구성하면 된다.
- 60 15 5 30 6 -50
- -5 -20 -5 275 50 0
- 125 11 2 20 -4 555
4 : 5555
- 1 +-*/ 3
- 2 +-*/ 2
- 3 +-*/ 1
5 : 55555
- 1 +-*/ 4
- 2 +-*/ 3
- 3 +-*/ 2
- 4 +-*/ 1

문제의 해결 일반화

n : “x”*n
- 1 +-*/ n-1
- 2 +-*/ n-2
- n-1 +-*/ 1
n-1번까지 사용해서 만들 수 있었던 수를 알아놨다고 하고, (부분 문제의 답은 알고 있다고 가정)
n번 늘어서는 것
그런데 이 문제에서 괄호도 사용할 수 있다. 그 처리는 어떻게 해줄까?
별 문제가 없다. 왜 그러냐면, 몇 번 사용해서 만든 수를 가지고 있을 때, 수식으로 가지고 있는게 아니라 수를 가지고 있다.
따라서 괄호를 친 것과 동일하다.
괄호 없이 쭉 수식을 만들어내면, 그 수들의 안에 포함이 될까? -> 그것 또 답은 그렇다. 완전하게 조합을 나타내기 때문에 계속해서 쌓아나가다 보면, 그 순서로 계산된 수식과 동등한 결과가 한번은 꼭 포함되도록 완전하게 나열을 했다.
5를 네번 사용했을 때와, 5번 사용했을 때는 가능한 수가 굉장히 많아진다.
그렇다면, 한 단계 늘어날 때마다, 굉장히 후보가 되는 수의 갯수가 많아진다.
얼마나 많이 커지는지 알아보기로 하자.

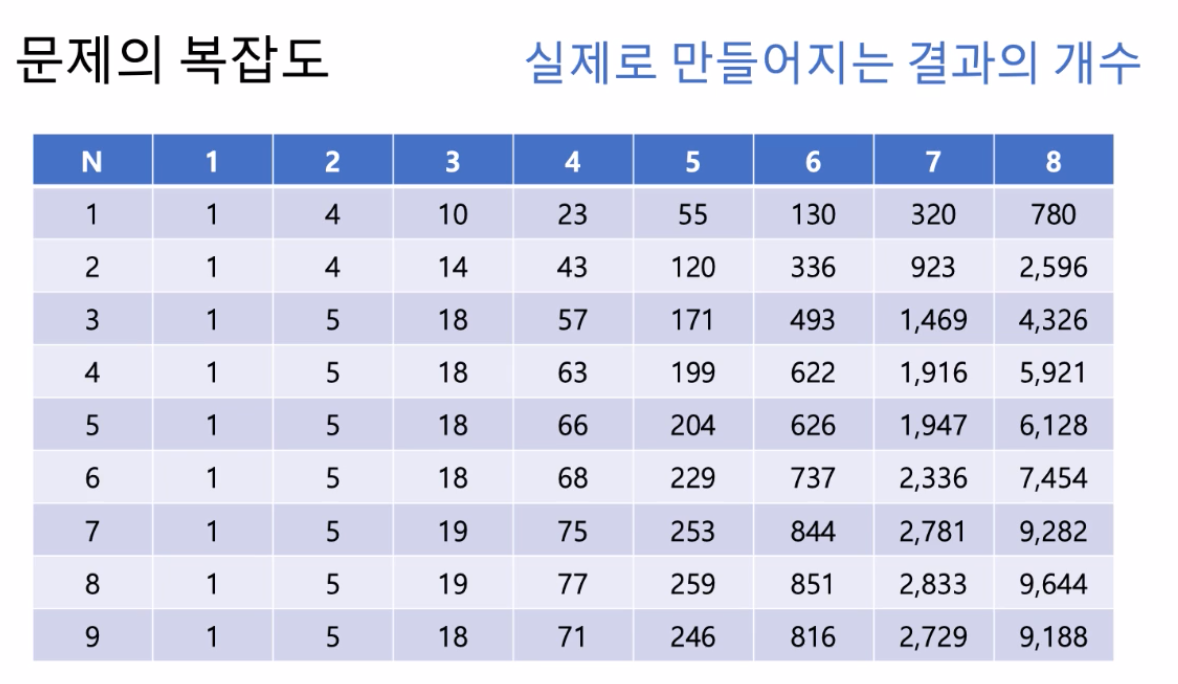
문제의 복잡도

(발생할 수 없는) 최악의 경우
숫자의 사용회수 1 - 만들어지는 결과의 수효 1
숫자의 사용회수 2 - 만들어지는 결과의 수효 5
숫자의 사용회수 3 - 만들어지는 결과의 수효 41
숫자의 사용회수 4 - 만들어지는 결과의 수효 429
숫자의 사용회수 5 - 만들어지는 결과의 수효 5073
숫자의 사용회수 6 - 만들어지는 결과의 수효 64469
숫자의 사용회수 7 - 만들어지는 결과의 수효 859385
숫자의 사용회수 8 - 만들어지는 결과의 수효 11853949
실제로 발생하는 것은 ?

요약

문제의 성질에 따라,
- 동적 계획법으로 풀어냄으로써
  - 탐색해야 하는 범위를 효과적으로 줄일 수 있음

풀어보기

def solution(N, number):
    s = [set()]*8
    # 여기서 [set()]*8하면 안된다. set이 하나 만들어진 뒤 8번 나열한 것이 나옴
    for i, x in enumerate(s, start=1):
        x.add(int(str(N)*i))  # 5,55,555,5555
    for i in range(1, len(s)):  # i라는 변수를 1부터 len(s)즉, s의 길이가 되기 전까지
        for j in range(i):  # i가 1이면 j는 0. i가 2이면 j는 0,1 i=3, j=0,1,2
             # j가 0,1,2로 변했다면 i-j-1은 2,1,0이 된다.
            for op1 in s[j]:  # 연산자의 앞에 놓일 피연산자 마련
                for op2 in s[i-j-1]:  # 연산자의 뒤에 놓일 피연산자 마련
                    s[i].add(op1 + op2)
                    s[i].add(op1 - op2)
                    s[i].add(op1 * op2)
                    if op2 != 0:  # 뒤의 숫자가 0이면 나눗셈 불가
                        s[i].add(op1 // op2)
                # 덧셈과 곱셈에 대해서, 더 줄여주고 싶다면, 7행의 j in range(i)에서 절반까지만 진행하게 한 뒤, 안에서 뺄셈과 나눗셈만 앞뒤 바꾼 걸 할 수도 있지만,
                # 그래봐야 얻을게 크지 않고 코드 가독성이 떨어진다. 그래서 이런 구조 채택

        if number in s[i]:
            answer = i+1
            break
    else:
        answer = -1
    return answer


print(solution(5, 12))

참고자료 [프로그래머스]https://programmers.co.kr/learn/courses/9877