SWE_python_Stack1

작성일 | In

1.Stack

목차

  1. Stack 자료구조의 개념
  2. Stack의 응용
  3. Memoization
  4. DP(동적계획법)
  5. DFS(깊이 우선 탐색)

1.1 Stack 자료구조의 개념

  1. 물건을 쌓아 올리듯 자료를 쌓아 올린 형태의 자료구조
  2. 스택에 저장된 자료 구조는 선형구조를 가짐
    • 선형구조 : 자료 간의 관계가 1대 1의 관계
    • 비선형 구조 : 자료 간의 관계가 1대 N의 관계를 가짐
  3. 스택에 자료를 삽입하거나 스택에서 자료를 꺼낼 수 있ㅇ므
  4. 마지막에 삽입한 자료를 가장 먼저 꺼냄
  5. 후입선출 : LIFO(Last-In-First-Out)

1.2 Stack 구현

  • 파이썬에서는 리스트를 사용할 수 있음
  • 저장소 자체를 스택이라고 부르기도 함

  • 스택에서 마지막 삽입된 원소의 위치를 top이라고 부름

  • 삽입 : push
  • 삭제 : pop
  • isEmpty: 스택이 공백인지 확인
  • peek: 스택의 top에 있는 원소를 반환

1.3 push 알고리즘

def push(item):
    s.append(item)

파이썬에서는 list를 활용한다.

  • list는 크기의 제한이 없으므로 overflow문제를 고려할 필요가 없고
  • 삽입할 마지막 위치를 기억할 top변수도 필요 없다. append method를 통해서 마지막에 삽입 가능하기 때문이다.

1.4 pop 알고리즘

def pop():
    if len(s) == 0:
        # underflow
        return
    else:
        return s.pop(-1)
  • top이 만약 -1이라면 -1 값은 top의 초기값을 의미. 스택에 자료가 없는 상태. 이 경우 underflow 처리를 한다.
  • 그렇지 않으면 탑의 값을 반환하고 1감소 시킨다
  • 리스트에서는 pop method를 통해서 마지막 값을 반환할 수 있다.
  • pop() 리스트의 맨 마지막 요소를 돌려주고 그 요소는 삭제한다
  • pop(x) 리스트의 x번째 요소를 돌려주고 그 요소는 삭제한다.
  • 이렇게 보니까 재귀함수 처럼 보여서 헷갈릴 수 있는데 pop은 내장함수야

1.5 스택 구현 고려사항

  • 리스트를 사용하여 스택을 구현하는 경우 : 구현이 용이하지만, 리스트의 크기를 변경하는 작업은 내부적으로 큰 overhead 발생 작업으로 많은 시간이 소요
  • 이를 해결하기 위해 리스트의 크기가 변동되지 않도록 배열처럼 크기를 미리 정해놓고 사용하는 방법과
  • 동적 연결리스트를 이용하여 저장소를 동적으로 할당하여 스택을 구현하는 방법이 있다.

2 Stack의 응용_괄호검사

  • 괄호의 종류 : 대괄호, 중괄호, 소괄호
  • 조건 : 1. 왼쪽 괄호의 개수와 오른쪽 괄호의 개수가 같아야 함
  • 조건 : 2. 같은 괄호에서 왼쪽 괄호는 오른쪽 괄호보다 먼저 나와야 함
  • 조건 : 3. 괄호 사이에는 포함 관계만 존재함

2.1 Stack의 응용

  • 스택을 이용한 괄호 검사
  • 여는 괄호이면 스택에 저장
  • 닫는 괄호이면 스택에 pop하여 비교

  • 괄호 수식이 끝났는데 스택에 괄호가 남아있으면 올바르지 못한 괄호.

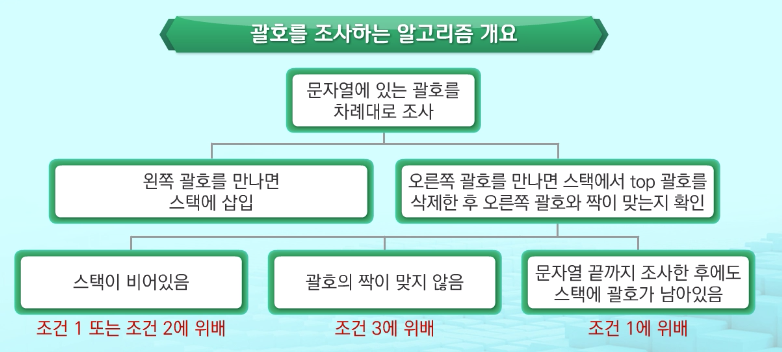
  • 괄호를 조사하는 알고리즘 개요 No Image

  • 스택이 비어있거나 짝이 맞지 않거나, 문자열 끝가지 조사한 후에도 괄호가 남아있거나 하면 문제!

2.2 함수 호출 관리

  • 프로그램에서의 함수 호출과 복귀에 따른 수행 순서를 관리
  • 함수 호출 발생시 호출한 함수 수행에 필요한 지역변수, 매개변수 및 수행 후 복귀할 주소 등의 정보를 스택 프레임에 저장
  • 함수의 실행이 끝나면 시스템 스택의 top 원소(스택 프레임)를 삭제(pop)하면서 프레임에 저장되어있던 복귀주소로 환원
  • 함수 호출과 복귀에 따라 이 과정을 반복하여 전체 프로그램 수행이 종료되면 시스템 스택은 공백 스택이 됨

2.3 재귀호출

  • 자기 자신을 호출하여 순환 수행되는 것
  • 함수에서 실행해야 하는 작업의 특성에 따라 일반적인 호출방식보다 프로그램의 크기를 줄이고 간단하게 작성 가능
  • 디버깅이 어렵고 잘못 작성하게 되면 수행 시간이 많이 소요됨
  • 재귀 호출을 작성할 수 있는 함수 - factorial: N! : 1부터 N까지의 모든 자연수를 곱하여 구하는 연산
  • n! = n x (n-1)!

3 Memoization

3.1 피보나치 수열

  • 재귀 호출을 작성할 수 있는 함수 - 피보나치 수열을 구하는 함수
  1. 0과 1로 시작하고 이전의 두 수 합을 다음 항으로 하는 수열 : 0, 1, 1, 2, 3, 5, 8, 13
  2. 피보나치 수열의 i번 째 값을 계산하는 함수 F를 정의하면 다음과 같음
    • F0 = 0, F1 = 1
    • Fi = F(i-1) + F(i-2) for i >=2
  3. 위의 정의로부터 피보나치 수열의 i번째 항을 반환하는 함수를 재귀 함수로 구현 가능

3.2 피보나치 수열을 구하는 함수의 알괼즘

def fibo(n):
    if n < 2 :
        return n
    else :
        return fibo(n-1) + fibo(n-2)

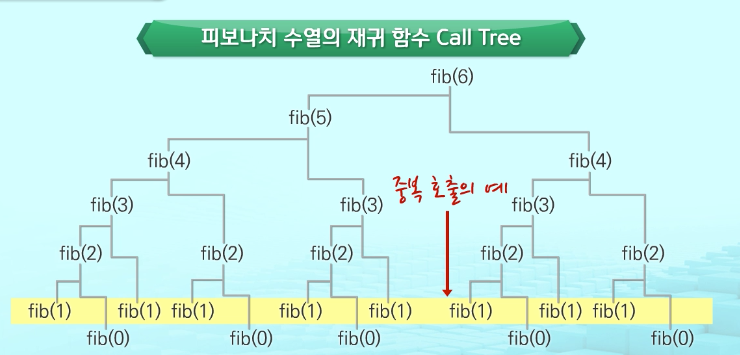
문제점 => 엄청난 중복 호출이 존재함 No Image

3.3 Memoization

  • 컴퓨터 프로그램을 실행할 떄 이전에 계산한 값을 메모리에 저장해서 매번 다시 계산하지 않도록 하여 전체적인 실행 속도를 빠르게 하는 기술
  • 동적 계획법(DP)의 핵심이 되는 기술
  • Memoization 단어의 의미: 글자그대로 ‘메모리에 넣기(to put in memory)’라는 의미
  • 기억되어야 할 것이라는 뜻의 라틴어에서 파생
  • Memorization (기억하기, 암기하기)와 혼동하지만 정확한 단어는 Memoization (동사형은 Memoize)

3.4 Memoization 방법을 적용한 알고리즘

  • 피보나치 수를 구하는 알고리즘에서 fibo(n)의 값을 계산하자마자 저장하면 실행시간을 줄일 수 있음
  • 만약 기존에 계산하여 저장된 값이 있을 경우 다시 계산하지 않겠다는 알고리즘
# memo를 위한 리스트를 생성하고
# memo[0]을 0으로 memo[1]는 1로 초기화 한다

def fibo1(n):
    global memo
    if n >= 2 and len(memo) <= n:
        memo.append(fibo1(n-1)+ fibo1(n-2))
    return memo[0]
memo = [0,1]


# 다른 분 코드를 참고


memo = {1: 1, 2: 1}

def fibonacci(n):
    if n == 0:
        return 0
    if n not in memo:
        memo[n] = fibonacci(n-1) + fibonacci(n-2)
    return memo[n]

print(fibonacci(3))
print(memo)


# 보다  파이썬스러운 방법
def fibonacci(n):
    a, b = 1, 0
    for i in range(n):
        a, b = b, a + b
    return b

4. DP 동적계획법

4.1 DP 알고리즘

  • Dynamic Programming의 약자
  • 그리지 알고리즘과 같이 최적화 문제를 해결하는 알고리즘
  • 먼저 입력 크기가 작은 부분 문제들을 모두 해결한 후에 그 해들을 이용하여 보다 큰 크기의 부분 문제들을 해결
  • 최종적으로 주어진 입력의 문제를 해결

4.2 피보나치 수를 구하는 함수에 DP 적용하기

  1. 문제를 부분 문제로 분할
  2. 부분 문제로 나누는 일을 끝냈으면 가장 작은 부분문제부터 해를 구함
  3. 그 결과는 테이블에 저장하고, 테이블에 저장된 부분 문제의 해를 이용하여 상위 문제의 해를 구함

4.3 피보나치 수를 DP에 적용한 알고리즘

def fibo2(n):
    f = [0,1]
    for i in range(2, n+1):
        f.append(f[i-1] + f[i-2])
    return f[n]

4.4 DP 구현 방식

  1. recursive방식 : fibo1()
  2. iterative 방식 : fibo2()

5. DFS(깊이 우선 탐색)

  1. 비선형 구조인 그래프 구조는 그래프로 표현된 모든 자료를 빠짐없이 검색하는 것이 중요
    • 깊이 우선 탐색 (Depth First Search, DFS)
    • 너비 우선 탐색 (Breadth First Search, BFS)

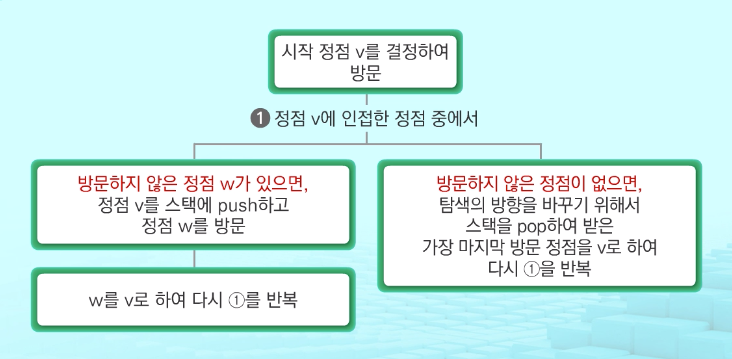
5.1 깊이 우선 탐색 방법

  1. 시작 정점의 한 방향으로 갈 수 있는 경로가 있는 곳까지 깊이 탐색
  2. 더 이상 갈 곳이 없게 되면, 가장 마지막에 만났던 갈림길 간선이 있는 정점으로 되돌아옴
  3. 다른 방향의 정점으로 탐색을 계속 반복하여 결국 모든 정점을 방문하여 순회
  4. 가장 마지막에 만났던 갈림길의 정점으로 되돌아가서 다시 깊이 우선 탐색을 반복해야 하므로 후입선출 구조의 스택을 사용

5.2 깊이 우선 탐색 알고리즘

No Image

visited[], stack[] 초기화
DFS(v)
    v 방문;
    visite[v] <- true;
    do{
        if(v의 인접 정점 중 방문 안한 w 찾기)
            push(v);
        while(w){
            w 방문;
            visited[w]<- true;
            push(w)
            v <- w
            v의 인접 정점 중 방문 안한 w 찾기
        }
        v<-pop(stack)
    }while(v)
end DFS()

5.3 DFS의 예

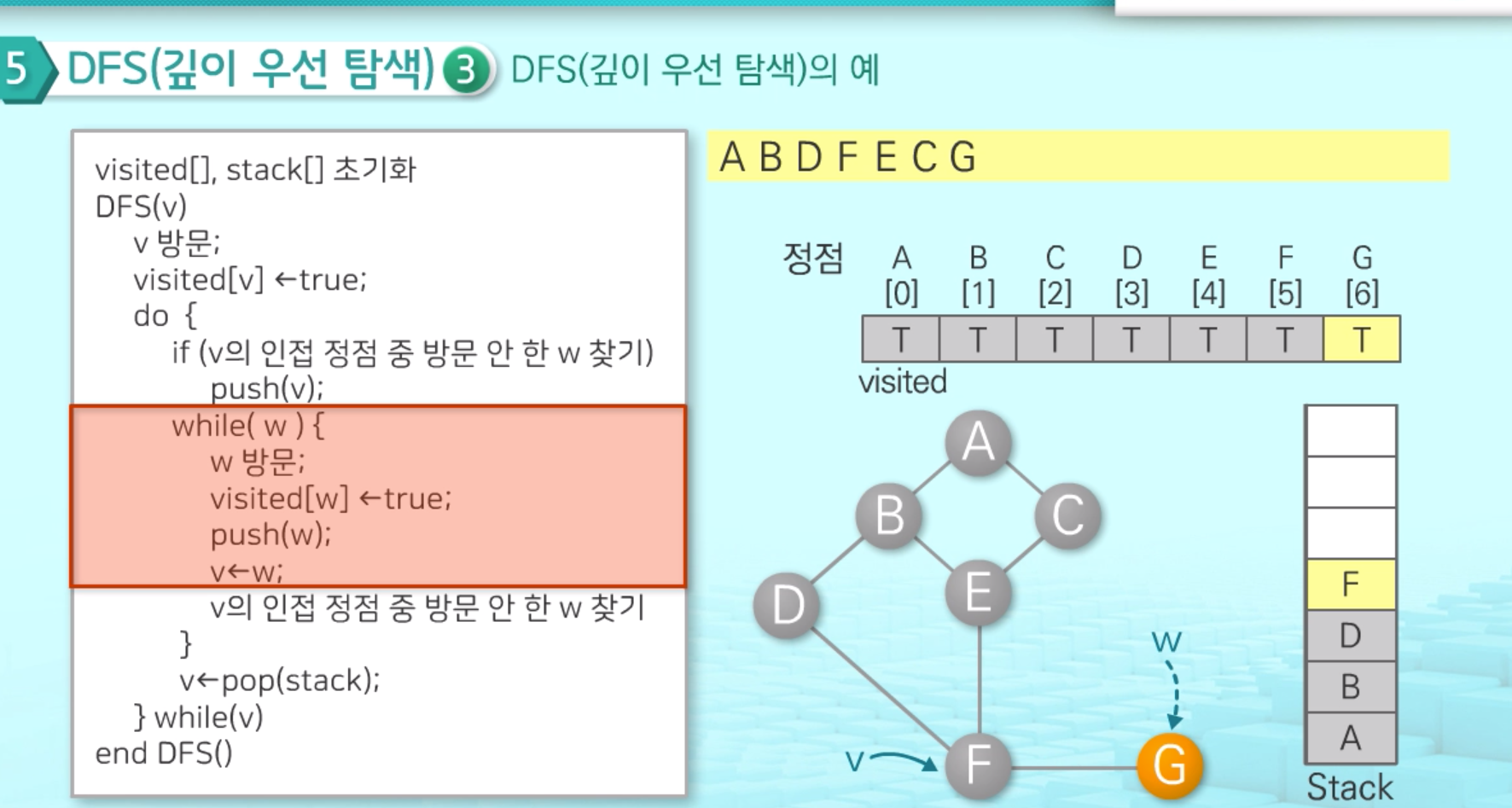
과정 설명만 5분이다. 어렵다. 과정을 동영상을 보면서 실제 구현할 때 더 이해하자. No Image

  • 탐색 순서를 살펴보면 ABDFECG임을 알 수 있다.
  • 한쪽 방향을 탐색하다가 더 이상 진행할 수 없으면 다시 되돌아 오는 방법으로 탐색했다는 것을 확인 가능
  • 다시 되돌아 오기 위해 사용한 자료구조로 스택을 사용했다는 것을 기억해야 함

참고자료 [SWE]https://swexpertacademy.com [피보나치 수열 참조 블로그]https://devdoggo.netlify.com/post/alg_ds/challenges/fibonacci_solutions/

0%