Python_List1(2)
목차
- 2차원 리스트 (이전 파일에 있음)
- 부분 집합
- 검색
- 정렬
2. 부분집합
유한 개의 정수로 이루어진 집합이 있을 때, 이 집합의 부분 집합 중에서 그 집합의 원소를 모두 더한 값이 0이 되는 경우가 있는 지를 알아내는 문제 예 {-7,-3,-2,5,8}
-3,-2,5는 부분집합이면서 합이 0이다. => 따라서 이 경우 참
- 완전 검색 기법으로 부분 집합의 합 문제를 풀기 위해서는 우선 집합의 모든 부분 집합을 생성한 후 각 부분 집합의 합을 계산함
- 주어진 집합의 부분 집합을 생성하는 방법 생각해 보기
부분 집합의 수
Q) 어떤 집합의 부분 집합을 구할 경우 부분 집합의 총 개수가 몇 개일까요 ?
- 집합의 원소가 n개 일 때, 공집합을 포함한 부분집합의 수는 2^n개
- 각 원소를 부분집합에 포함시키거나 포함시키지 않는 2가지 경우를 모든 원소에 적용한 경우의 수와 같음 ex) {1,2,3,4} => 2x2x2x2 => 16가지
Loop를 이용하여 확인하고, 부분 집합을 생성하는 방법

비트연산자
0과 1로 이루어진 이진수에 대한 연산을 수행하는 연산자 {&, |, «, »}
<<연산자 활용하여 1<<n:2^n즉 원소가 n개일 경우의 모든 부분 집합의 수를 의미i & (1<<j):1i에서 j번째 비트가 1인지 아닌지를 리턴함
비트 연산을 활용한 부분 집합을 생성하는 방법
arr = [3,6,7,1,5,4]
n = len(arr) # n: 원소의 개수
for i in range(1<<n) : # 1<<n: 부분집합의 개수
for j in range(n): # 원소의 수만큼 비트를 비교함 (원소의 포함 여부 판단이 가능)
if i & (1<<j): # i의 j번째 비트가 1이면 j번째 원소 출력
print(arr[j],end=",")
print()
3. 검색
저장되어 있는 자료 중에서 원하는 항목을 찾는 작업 원하는 항목:목적하는 탐색키를 가진 항목 탐색키: 자료를 구별할 수 있는 키
검색의 종류
- 순차 검색
- 이진 검색
- 인덱싱
순차 검색
- 일렬로 되어있는 자료를 순서대로 검색하는 방법
- List나 연결 List 등 순차구조로 구현된 자료구조에서 유용함
- 구현이 쉽지만, 검색 대상이 많은 경우 수행 시간의 증가로 비효율적임
- 2가지 경우가 있음
- 정렬된 경우
- 정렬되지 않은 경우
정렬되지 않은 자료의 검색 과정
첫 번째 원소부터 순서대로 검색대상과 키 값이 같은 원소가 있는지를 비교하여 찾음 키 값이 동일한 원소를 찾으면 그 원소의 인덱스를 반환 자료구조의 마지막에 갈 때까지 검색 대상을 찾지 못하면 검색 실패
찾고자 하는 원소의 순서에 따른 비교횟수 결정
n개에서의 순차 검색의 평균 비교 횟수는 n+1/2. 따라서 시간 복잡도는 : O(n)
def sequentialSearch(a,n,key):
i = 0
while i < n and a[i]!= key:
i = i + 1
if i < n : return i
else: return -1
정렬된 자료의 검색 과정
- 자료가 오름차순으로 정렬된 상태에서 검색을 실시한다고 가정
- 자료를 순차적으로 검색하면서 키 값을 비교함
- 원소의 키 값이 검색 대상의 키 값보다 크면 원소가 없다는 것이므로 더 이상 검색하지 않고 검색을 종료함
- 정렬되어 있으므로, 검색 실패를 반환하는 경우 평균 비교 회수가 반으로 줄어듦
- 시간 복잡도는 : O(n)으로 동일
def sequentialSearch2(a,n,key):v
i = 0
while i < n and a[i]< key:
i = i + 1
if i < n and a[i] == key : return i
else: return -1
이진 검색
자료의 가운데 항목의 키 값과 비교하여 다음 검색의 위치를 결정하고 검색을 계속하는 방법 목적 키를 찾을 때까지 이진 검색을 순환적으로 반복 수행함으로써 검색 범위를 반으로 줄여가며서 빠르게 검색을 수행함 이진 검색을 하기 위해서는 자료가 정렬된 상태여야 함 정렬된 데이터 n개가 있는 경우의 시간복잡도 순차 O(log N)
이진 검색 과정
- 자료의 중앙에 있는 원소 선택
- 중앙 원소의 값과 찾고자 하는 목표 값을 비교
- 목표값 < 중앙 원소 값 : 자료의 왼쪽 반에 대해서 새로 검색을 수행 목표값 > 중앙 원소 값 : 자료의 오른쪽 반에 대해서 새로 검색을 수행 찾고자 하는 값을 찾을 때까지 [1~3]의 과정을 반복
검색 범위의 시작점과 종료점을 이용
- 검색 범위의 시작점과 종료점을 이용하여 검색을 반복 수행함
- 이진 검색의 경우 자료에 삽입이나 삭제가 발생하였을 때 List의 상태를 항상 정렬 상태로 유지하는 추가 작업이 필요함
아래는 이진 검색의 알고리즘
def binarySearch(a,key):
start = 0
end = len(a)-1
while start <= end:
middle = start + (end - start) //2
if key == a[middle]: # 검색 성공
return True
elif key < a[middle]:
end = middle -1
else :
start = middle + 1
return False # 검색 실패
재귀 함수를 이용한 이진 검색 구현
def binarySearch2(a, low, high, key):
if low > high : # 검색 실패
return False
else:
middle =(low + high) //2
if key == a[middle] : # 검색 성공
return True
elif key < a[middle]:
return binarySearch2(a, low, middle-1, key)
elif a[middle] < key:
return binarySearch2(a, middle+1, high, key)
인덱스
- 데이터베이스에서 유래, 테이블에 대한 동작 속도를 높임
- 룩 업 테이블 등의 용어로 사용함
- 인덱스를 저장하는데 필요한 디스크 공간은 보통 테이블 저장에 필요한 디스크 공간보다 작음
- 인덱스는 키 - 필드만 갖고 있고, 테이블의 다른 세부 항목은 갖고 있지 않음
- List를 사용한 인덱스 : 대량의 데이터를 매번 정렬하면 프로그램의 반응은 느려질 수 밖에 없음. 이러한 대량 데이터의 성능 저하 문제를 해결하기 위해 List 인덱스를 사용할 수 있음
4. 정렬
셀렉션 알고리즘의 의미
- 저장되어 있는 자료로부터 k번째로 큰 혹은 작은 원소를 찾는 방법
- 최소값, 최대값 혹은 중간값을 찾는 알고리즘을 의미하기도 함
- 셀렉션 선택 과정 : 정렬 알고리즘을 이용하여 자료를 정렬 -> 원하는 순서에 있는 원소 가져오기
ex) k번째로 작은 원소를 찾는 알고리즘
1번부터 k번째까지 작은 원소들을 찾아 List의 앞쪽으로 이동시키고, List의 k번째를 반환 k가 비교적 작을 때 유용하며 O(kn)의 수행시간을 필요로 함
def select(list,k):
for i in range(0, k):
minIndex = i
for j in range(i+1, len(list)):
if list[minIndex] > list[j]:
minIndex = j
list[i], list[minIndex] = list[minIndex], list[i]
return list[k-1]
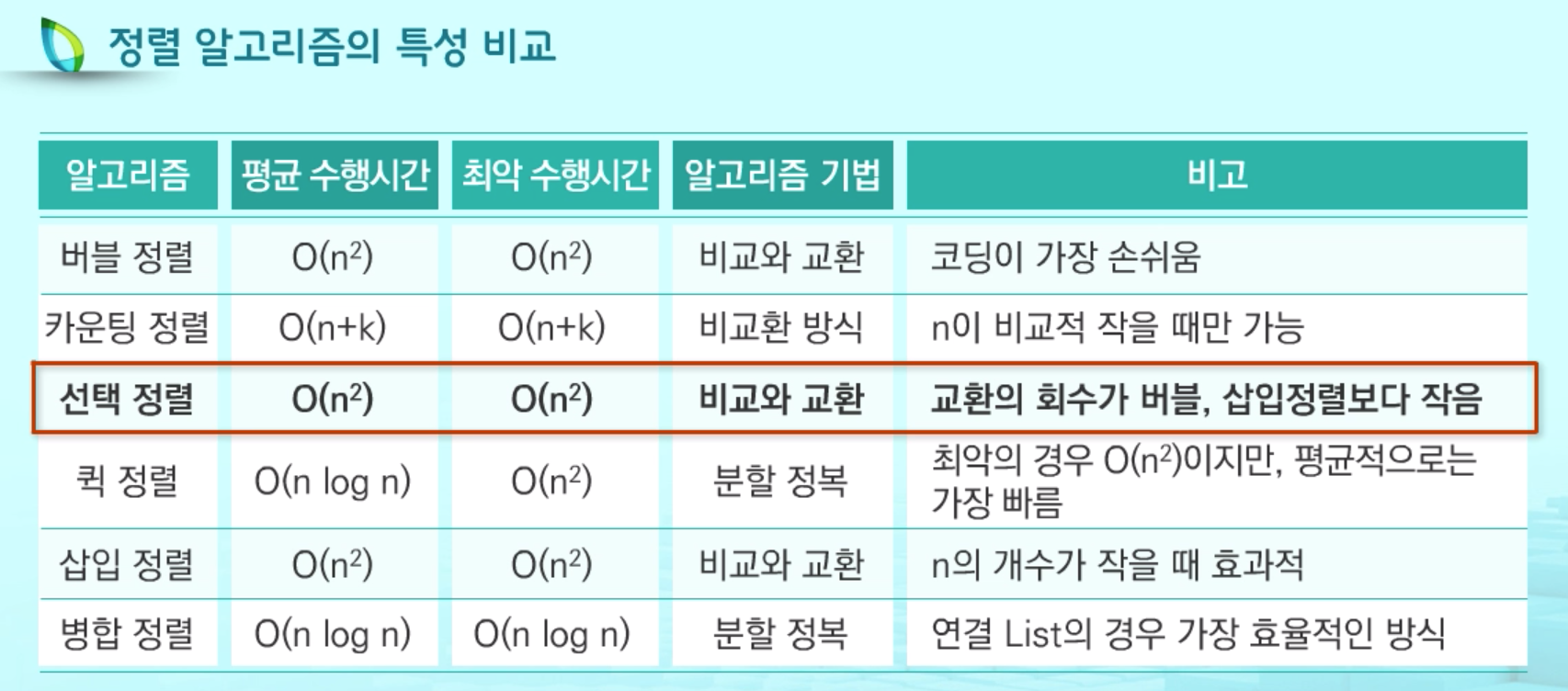
선택 정렬
포켓본 순서대로 정렬하기
- 주어진 자료들 중 가장 작은 값의 원소부터 차례대로 선택하여 위치를 교환하는 방식
- 셀렉션 알고리즘을 전체 자료에 적용한 것
정렬과정
- 주어진 List 중에서 최소값을 찾음
- 그 값을 List의 맨 앞에 위치한 값과 교환
- 맨 처음 위치를 제외한 나머지 List를 대상으로 위의 과정을 반복
시간 복잡도 O(n^2)
선택정렬 알고리즘 슈도코드
def selectionSort(a):
for i in range(0,len(a)-1):
min = i
for j in range(i+1, len(a))
if a[min]>a[j]:
min = j
a[i], a[min] = a[min], a[i]
참고자료 [SWE]https://swexpertacademy.com