SWE_python

Python_List1(1)

1.Python 기초 정리

인터프리터 언어 -> 느리지만 독립적인 플랫폼
객체 지향
IoT, AI에 자주 이용

무엇이 좋은 알고리즘인가 ?
- 정확성, 작업량(적은 연산), 메모리 사용량, 단순성, 최적성(개선의 여지)
성능 분석 -> 실행되는 명령문의 갯수를 계산
빅오 표기법

변수

파이썬에서 모든 자료는 객체다. Java나 C에서 사용되는 기본형 타입 변수도 파이썬에서는 객체다.
변수의 선언이 따로 없다. -> 변수에 값을 초기화시 변수 메모리에 생성한다 -> 하나의 변수에 다른 타입의 값을 저장할 수 있다. (모든 변수는 참조형 타입에 속한다)

자료형

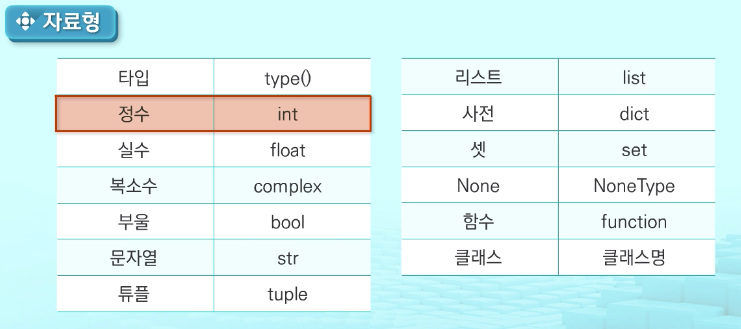
type() : 변수에 저장된 데이터 확인 가능
int() : 제한이 없다. 메모리가 허용되는 한 무한의 값 저장 가능

컨테이너

언어 level에서 자료구조를 지원한다

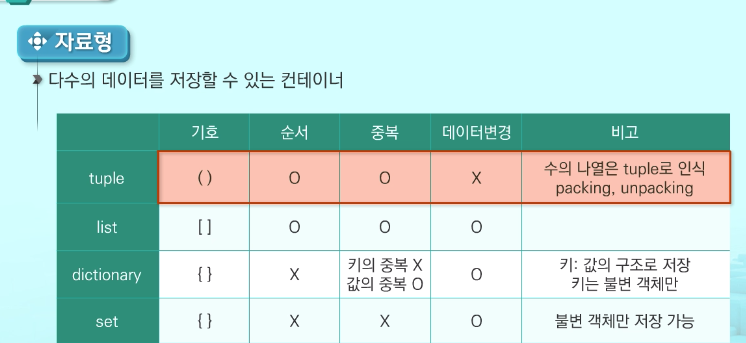
paking : 데이터를 ,로 나열하는 작업(튜플로 만드는 작업)
unpaking : 튜플에 묶여있는 데이터를 낱개로 꺼내는 작업
list와 tuple처럼 순서가 있는 자료형은 중복이 허용 가능하다.
속도 : list < tuple

List

배열 : 같은 타입 변수들을 하나의 이름으로 열거하여 사용하는 자료구조 리스트는 C와 Javad에서의 배열과 비슷

사용법

파이썬의 변수는 별도의 선언 방법x -> 변수에 처음 값을 할당할 때 생성.
Q) 값을 초기화 하기 전에, 변수를 미리 만들어야 하는 경우는?
공백 리스트 생성
1. num = []
2. arr = list()
시퀀스 자료형 : 인덱싱과 슬라이싱 모두 사용 가능
- 인덱싱 : 시퀀스 자료형에서 하나의 요소를 연산자를 통하여 참조하는 것
- 시퀀스 자료형의 원하는 범위를 선택하는 연산
- ex) arr=[4,5,6,7,8,9] arr[1:3] #[5,6] (시작: 포함, 끝: 포함x)

내장함수

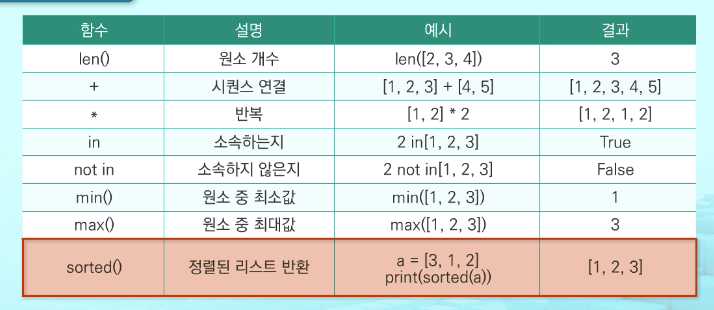
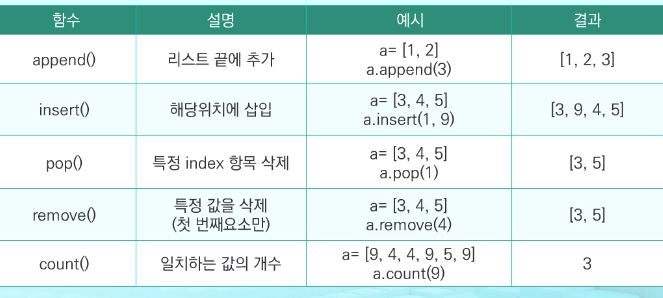
리스트 함축

2.완전검색 (Exhaustive Search)

Brute-force or Generate-and-Test 기법이라고도 불림
모든 경우의 수를 test한 후, 최종해법 도출
완전검색으로 해답 도출 후, 다른 알고리즘을 사용하는게 바람직
ex) Baby-gin 게임

BabyGin 해결 방법

고려할 수 있는 모든 경우의 수 생성(중복 포함)
앞 3 / 뒤 3으로 잘라서 run, triplet test

순열

서로 다른 것 중 몇 개를 뽑아서 한 줄로 나열 한 것

3.greedy 알고리즘

최적해를 구하는데 사용되는 근시안적인 방법 -> 여러 경우 중 하나를 선택할 때마다, 그 순간에 최적이라고 생각되는 것을 선택해 나가는 방식으로 진행

해 선택 : 현재 상태에서 부분 문제의 최적해를 구한 뒤, 이를 부분 해 집합에 추가
실행 가능성 검사 : 새로운 부분 해 집합에 실행 가능한 지를 확인, 곧 문제의 제약조건에 위배되지 않았는지 검사
해검사 : 새로운 부분해 집합이 문제의 해가 되는지를 확인, 전체 문제의 해가 완성 되지 않았다면 해 선택부터 다시

ex) 거스름돈 줄이기

Baby-gin을 Greedy로 풀어보기

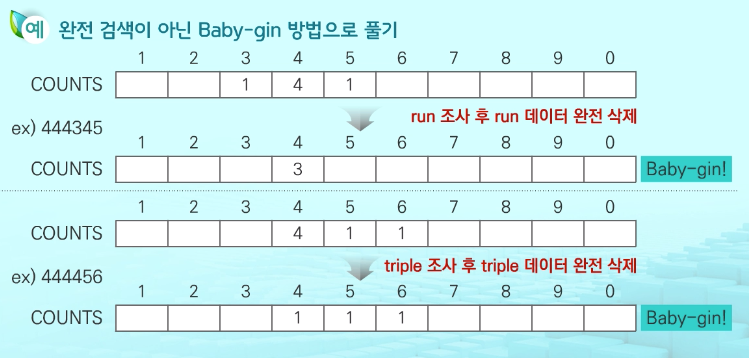
Greedy 알고리즘의 한계

정렬

정렬 : 2개 이상의 자료를 특정 기준에 의해 작은 값부터 큰 값 혹은 그 반대의 순서대로 재배열하는 것 정렬에서 키란 자료를 정렬하는 기준이 되는 특정 값을 의미한다

버블 정렬
카운팅 정렬
선택 정렬
퀵 정렬
삽입 정렬
병합 정렬

버블 정렬

인접한 두 개의 원소를 비교하며 자료를 계속 교환하는 방식

첫 번쨰 원소부터 인접한 원소끼리 자리 교환하면서 맨 마지막 까지 이동
한 단계가 끝나면 가장 큰 원소 또는 가장 작은 원소가 마지막 자리로 정렬됨
마지막 단계까지 반복

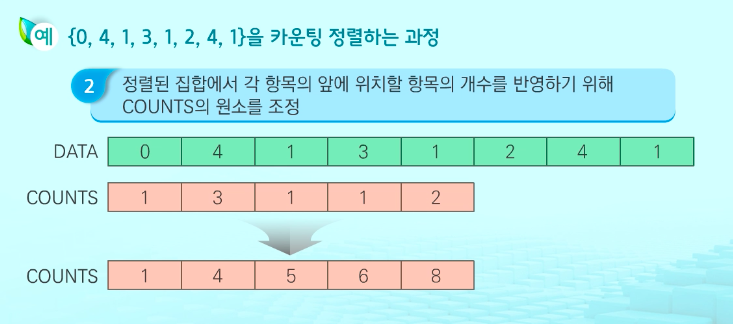
카운팅 정렬

항목들의 순서를 결정하기 위해 집합에 각 항목이 몇 개씩 있는지 세는 작업을 하여, 선형 시간에 정렬하는 효율적인 알고리즘

앞의 항목의 개수를 카운트리스트 항목에 더하게 된다. 해당 원소가 정렬될 때, 리스트이 몇 번째 위치에 들어가야 하는 지를 보여줌 -> 이를 조금더 쉽게 말하면

ex) A=[2,0,2,0,4,1,5,5,2,0,2,4,0,4,0,3]

C=[5,1,4,1,3,2]

c의 직전 요소의 값을 다 더하면 다음과 같다.

C=[5,6,10,11,14,16]

위 의미는, 원래 정렬될 배열에 b1부터 b16까지의 순서라고 했을 때

c1 = 5 : 0은 b1에서 b5까지 다섯개 자리를 차지한다.
c2 = 6 : 1은 b6 한 개 자리를 차지한다.
c3 = 10 : 2는 b7에서 b10까지 네 개의 자리를 차지한다.
c4 = 11 : 3은 b11 한 개 자리를 차지한다
c5 = 14 : 4은 b12에서 b14까지 두 개 자리를 차지한다
c6 = 16 : b15에서 b16까지 두 개 자리를 차지한다

이제 A의 요소값의 역순으로 B에 채운다. 예를 들어 3은 b11d의 한 개 자리를 차지하므로 b11에 넣고,자리가 하나 채워졌으므로 c3의 현재값(11)에서 1을 뺀다.
이와 같은 방식을 이용하는 것이다.

참고자료 [SWE]https://swexpertacademy.com

[카운팅 정렬]https://ratsgo.github.io/data%20structure&algorithm/2017/10/16/countingsort/

SWE_python_List1