목차
목차
- 트리
- 이진트리
- 이진트리 - 넓이 우선 순회 알고리즘
17. 트리
트리를 이해하고 관련 알고리즘 설계 구현에 필요한 개념 용어 설명
- 트리 : 정점(node)과 간선(edge)을 이용하여 데이터의 배치 형태를 추상화한 자료 구조
-
나무 : 뿌리(root), 이파리(leaf). 일반적으로 나무를 뒤집어서 생각한다.
- 가장 맨 위의 노드. 뿌리 -> 루트
- 이파리. leaf 노드.
- root도 leaf도 아닌 노드 -> internal node
부모 노드와 자식 노드
- 같은 부모 아래 child로 달려있는 노드들을 sibiling (형제 노드)관계에 있다고 부른다.
- 부모의 부모 (의 부모의 …)- 조상(ancestor)
- 자식의 자식 (의 자식의 …) - 후손(descendant)
노드의 수준 (Level)
- 루트노드는 레벨 0 (어떤 책에서는 1 부터)
- 아래로 한 단계 내려갈수록 레벨 증가.
트리의 높이 (Height)
- 트리의 높이 (height) = 최대 수준 (level) +1
- 깊이라고도 함 (depth)
부분 트리 (subtree)
- 서브트리가 몇개 있느냐에 따라 노드의 차수가 정해진다.
- = 자식(서브트리)의 수
이진 트리(Bianry Tree)
- 모든 노드의 차수가 2이하인 트리
- 재귀적으로 정의할 수 있음
- 빈 트리이거나 루트노드 + 왼쪽 서브트리 + 오른쪽 서브트리 ( 단, 이 떄 왼쪽과 오른쪽 서브트리 또한 이진트리)
포화 이진 트리 (Full Binary Tree)
- 모든 레벨에서 노드들이 모두 채워져 있는 이진 트리
- 높이가 k이고 노드의 개수가 2^k-1인 이진트리
완전 이진 트리 (Complete Binary Tree)
- 높이 k인 완전 이진 트리
- 레벨 k-2까지는 모든 노드가 2개의 자식을 가진 포화 이진 트리
- 레벨 k-1에서는 왼쪽부터 노드가 순차적으로 채워져 있는 이진 트리
18강 이진 트리
이진 트리의 추상적 자료 구조
- 연산의 정의
- size()
- depth()
- 순회(traversal)
이진 트리의 구현 - 노드(Node)
class Node:
def __init__(self,item):
self.data = item
self.left = None
self.right = None
class BinaryTree :
def __init__(self,r):
self.root=r
# size()
# 재귀적인 방법으로 쉽게 구할 수 있음!
# 터미널 컨디션만 주의하면 된다.
# 전체 이진 트리의 사이즈는 : left subtree의 사이즈 + right subtree의 사이즈 +1 (자기자신)
# 이 방법을 recursive하게 적용하면 전체 사이즈를 구할 수 있다.
class Node
def size(self):
# 왼쪽 노드가 있으면 사이즈 구하고 없으면 0으로 정의
l = self.left.size() if self.left else 0
# 오른쪽 노드가 있으면 사이즈 구하고 없으면 0으로 정의
r = self.right.size() if self.right else 0
return l + r + 1
clas BinaryTree:
def size(self):
if self.root:
return self.root.size()
else:
return 0
# depth() 역시 재귀적인 방법으로 쉽게 구할 수 있음!
# 전체 이진트리의 depth() = left subtree의 depth()와 right subtree()의 depth() 중 더 큰 것을 취한다음에 +1을 해주면 된다.
# 이건 연습문제
이진 트리의 순회
- 깊이 우선 순회 (depth first traversal)
- 중위 순회 (in-order traversal)
- 전위 순회 (pre-order traversal)
- 후위 순회 (post-order traversal)
- 넓이 우선 순회 (breath first traversal)
중위 순회
- (1) Left subtree
- (2) 자기 자신
- (3) Right subtree
class Node:
def inorder(self):
traversal = []
if self.left:
traversal += self.left.inorder()
traversal.append(self.data)
if self.right:
traversal += self.right.inorder()
return tarversal
class BinaryTree:
def inorder(self):
if self.root:
return self.root.inorder()
else:
return []
전위 순회 후위 순회는 연습 문제
전위 순회
- 자기 자신
- Left subtree
- Right subtree
후위 순회
- Left subtree
- Right subtree
- 자기자신
depth 구하기
class Node:
def __init__(self, item):
self.data = item
self.left = None
self.right = None
def size(self):
l = self.left.size() if self.left else 0
r = self.right.size() if self.right else 0
return l + r + 1
def depth(self):
l = self.left.depth() if self.left else 0
r = self.right.depth() if self.right else 0
return max(l,r)+ 1
class BinaryTree:
def __init__(self, r):
self.root = r
def size(self):
if self.root:
return self.root.size()
else:
return 0
def depth(self):
if self.root:
return self.root.depth()
else:
return 0
def solution(x):
return 0
preOrder
class Node:
def __init__(self, item):
self.data = item
self.left = None
self.right = None
def inorder(self):
traversal = []
if self.left:
traversal += self.left.inorder()
traversal.append(self.data)
if self.right:
traversal += self.right.inorder()
return traversal
def preorder(self):
traversal = []
traversal.append(self.data)
if self.left:
traversal += self.left.preorder()
if self.right:
traversal += self.right.preorder()
return traversal
def postorder(self):
traversal = []
if self.left:
traversal += self.left.postorder()
if self.right:
traversal += self.right.postorder()
traversal.append(self.data)
return traversal
class BinaryTree:
def __init__(self, r):
self.root = r
def inorder(self):
if self.root:
return self.root.inorder()
else:
return []
def preorder(self):
if self.root:
return self.root.preorder()
else:
return []
def postorder(self):
if self.root:
return self.root.postorder()
else:
return []
def solution(x):
return 0
19. 이진트리 - 넓이 우선 순회 알고리즘
- 지난 시간 : 깊이 우선 순회 방식 세 가지
- 넓이 우선 순회를 살펴보고 연습문제로, 메소드 구현
-
원칙
- 수준이 낮은 노드를 우선으로 방문 (낮은 수준부터 넓이를 우선으로 하나씩 방문)
- 같은 수준의 노드들 사이에는
- 부모 노드의 방문 순서에 따라 방문
- 왼쪽 자식 노드를 오른쪽 자식보다 먼저 방문
- Q) 재귀적 방법이 적합한가? -> 적합하지 않다.
-
넓이 우선 순회에서는 가장 낮은 레벨 부터 방문. -> 루트노드부터.
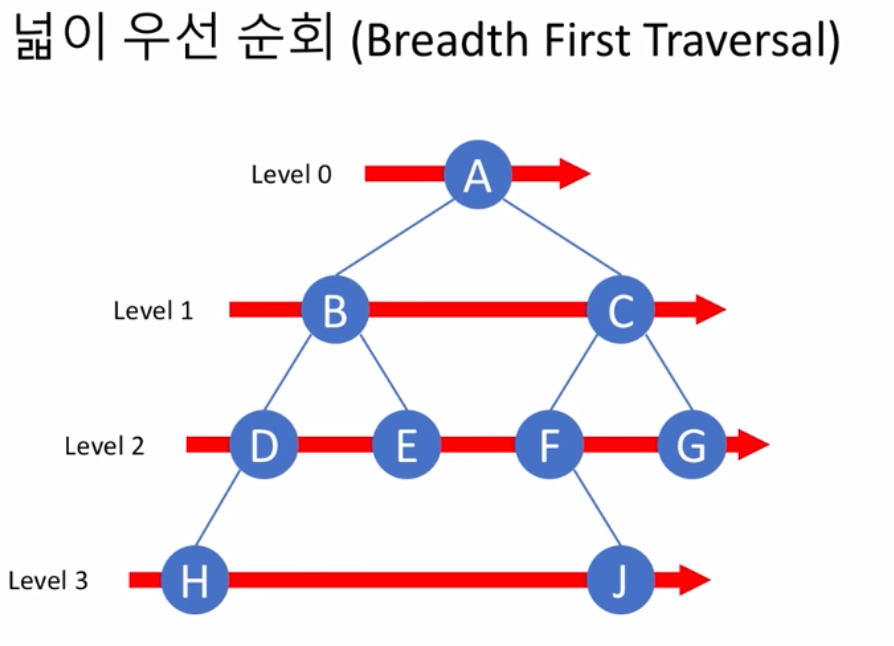
-
결국 순회 결과는 A-B-C-D-E-F-G-H-J
- 한 노드를 방문했을 때
- 나중에 방문할 노드들을 순서대로 기록해 두어야
- 큐를 이용하면 어떨까?
넓이 우선 순회 알고리즘의 설계
- 루트노드를 Queue에 넣고 시작
- 큐에서 하나씩 노드 꺼내면 처리! A 방문
- A방문할 때, 왼쪽과 오른쪽에 자식이 있다면 각각 큐에 넣는다 (B가 먼저 들어가고 다음 C가 들어간다)
- 이렇게 하면 노드 A의 처리 끝
- 그러면 queue에서 노드를 뽑아낸다. (B가 출력된다.)
- B방문. B도 자식들이 있다. 왼쪽 자식인 D를 큐에 넣고, E를 큐에 넣는다.
- 그럼 노드 B처리 끝 . 그럼 또 큐에서 하나의 원소를 뽑아본다. (C가 출력된다.)
- C방문. C도 자식들이 있다. 왼쪽 자식인 F와 G를 큐에 넣는다.
- Queue에는 D,E,F,G의 노드가 들어있다. 이건 레벨 2의 노드를 순서대로 기록한 것이다.
- Queue에서 노드를 꺼내서 D가 꺼내지니 D를 방문하고, 왼쪽 자식이 하나 있으니 H를 queue에 넣는다
- E를 꺼내서 방문. 자식이 없으니, 하나 꺼내서 F방문. 자식 j노드를 Queue에 집어 넣는다. 처리 끝났으므로 G 처리. 방문. 끝
- 남은 J. 꺼내서 처리 끝
- Queue가 비어있으면 모든 노드 처리 끝.
- 즉 Queue를 이용해서 다음에 이용할 노드들 기억 가능해짐
넓이 우선 순회 알고리즘 구현
class BinaryTree:
def bft(self):
- (초기화) traversal <- 빈 리스트, q <- 빈 큐(초기화)
- 빈 트리가 아니면, root node를 큐에 추가 (enqueue)
- q가 비어있지 않은 동안
-
- node <- q에서 원소를 추출 (dequeue)
-
- node를 방문
-
- node의 왼쪽, 오른쪽 자식 (있으면)들을 q에 추가
-
- q가 빈큐가 되면 모든 노드의 방문 완료
실습 답안
def bft(self):
q = ArrayQueue()
traversal = []
if self.root:
q.enqueue(self.root)
while not q.isEmpty():
node = q.dequeue()
traversal.append(node.data)
if node.left:
q.enqueue(node.left)
if node.right:
q.enqueue(node.right)
return traversal
참고자료 [파이썬_자료구조_알고리즘]https://programmers.co.kr/learn/courses/57